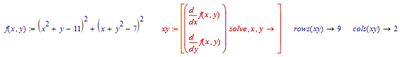Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbol math Prime and Mathcad 15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbol math Prime and Mathcad 15
I'm trying to parse a test function https://en.wikipedia.org/wiki/Himmelblau%27s_function using symbolic math. It has one local maximum, four global minimums and four saddle points.
Why does Prime's symbolic math only output the minimums? Mattcad 15 symbolic engine produces the traditional answer - absolutely accurate and absolutely indigestible.
Thanks for any response and comments. Attached files.
- Labels:
-
Algebra_Geometry
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
IMattcad 15 symbolic engine produces the traditional answer - absolutely accurate and absolutely indigestible.
"absolutely indigestible" ???
Not, if you add "assume, ALL=real"
BTW, you should show as partial derivative - at least in MC15 we can do that.
"absolutely accurate"
Unfortunately - No. (0; 0) is not a solution!
If you want to to SEE the result in Prime, you would have to add "simplify" or "simplify, max" and to get rid of the vanishingly small imaginary part you can use Ro:=Re(Ro). Its not nice to have to do that, but at least its a workaround.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, but the system has 9 real roots not 4 or 5 roots!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Sorry, but the system has 9 real roots not 4 or 5 roots!
You don't have to be sorry 😉
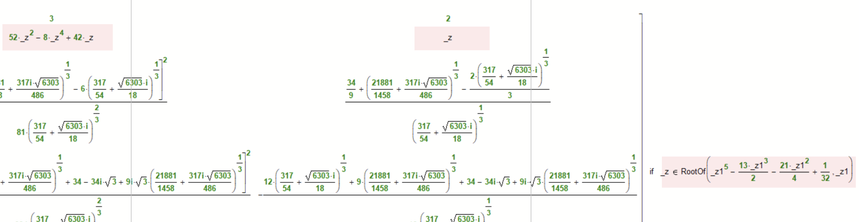
On contrary to Prime, Mathcad 15 tries at least to bring you the missing 5 solutions, too, but it fails to solve the fifth order equation exact symbolically
Interestingly you can try to solve this equation symbolically in a separate region and Mathcads symbolic switches to float mode and gives you the five real solutions for the y-ccordinates:
I have no idea why Mathcad wrongly returns (0; 0) as additional solution if we add the "assume, ALL=real" constraint. 😞
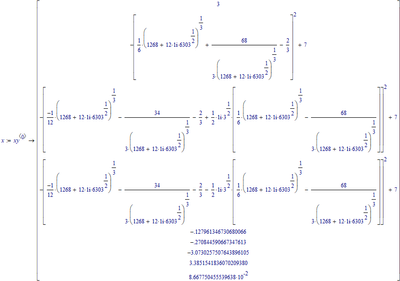
Of course you get all nine solutions in one go if you force the symbolic in float mode. This time also MC15 runs into numerical inaccuracies and returns tiny imaginary parts wihch you have to et rid of.
It would be interesting to see if MC11 with Maple can do a better job here (concerning exact symbolic solutions).
In case Luc is willing to give it a try, I attach the relevant parts in MC11 format.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
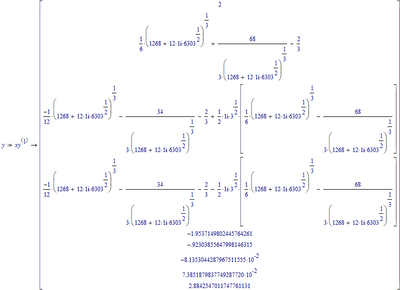
Mathcad 11/Maple:
(It's red because the numeric processor complains, because of the brackets surrounding the symbolic evaluation).
Means we have 9 solution pairs for x,y. The x's are:
The y's are:
And numerical approximation gives:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting! So MC11/Maple switches to float mode partially when it can't solve part of an equation in pure symbolics.
Its irritating that the exact solutions are the ones with a small imaginary part when evaluated numerically.
I guess that a symbolic evaluation with float could avoid that (actually it doesn't in MC15).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Tanks Luc!
Maple 2021
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The picture made with MC15 does not at all resemble the Prime pic you posted in your initial post (its not included in the Prime file you posted).
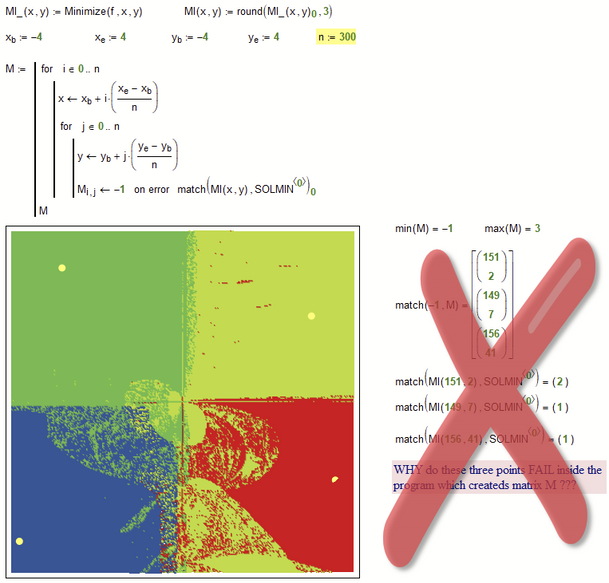
I tried to tidy up your worksheet an experienced a very unusual effect.
When I change the algorithm for "minimize" from "Quasi Newton" to "Conjugate Gradients", minimize fails for three points inside the program, but when I call it outside the program, no error occurs.
Has anybody an explanation for this?
EDIT: Yes, me! 🙂 The matrix indices are not the x- and y-values of the points. So outside of the program I was calling the function with the wrong input values. Thats the simple explanation why no error was thrown - silly me!
BTW, in case anybody is interested: Its not the solve block which fails for these three points but the problem is that the result of the solve block is too inaccurate and does not match to the precalculated value rounded to three decimals:
MC15 sheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
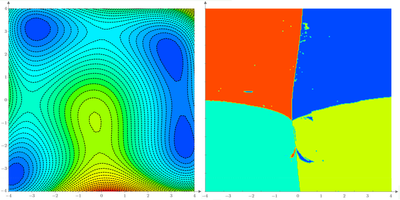
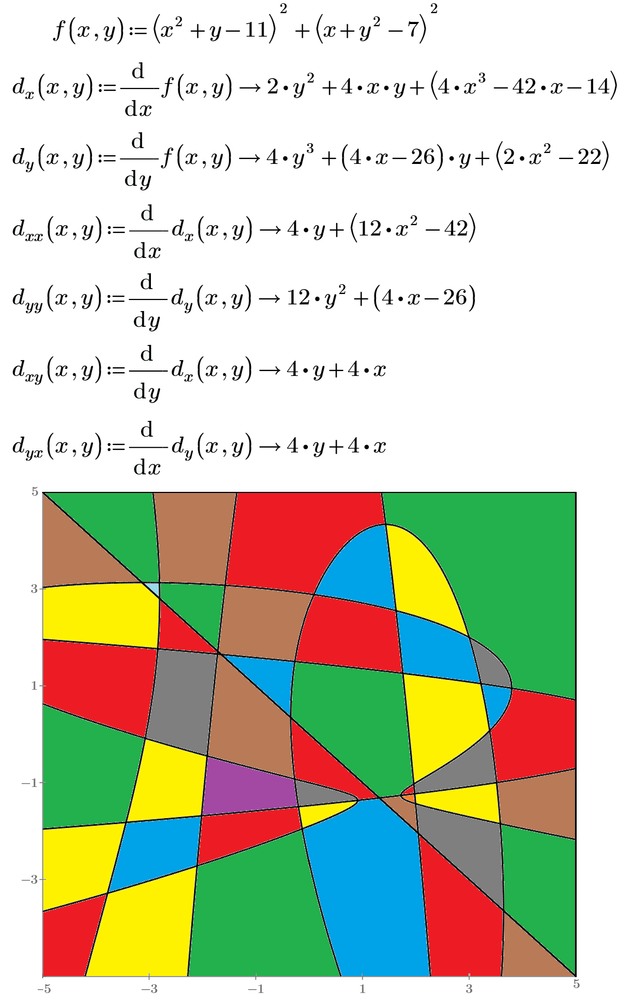
If you change the program to not just look for the minima but for all nine solutions for both derivaties be zero, you get a nice modern art pic.
Here I used "Find" with the LM-algorithm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Telepathy!
I just thought about the portrait of the nine roots of a system of two equations with two unknowns, when Werner immediately drew it and added nine bullet holes. Pushkin has a story on this subject The Shot (Pushkin) - Wikipedia
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My pictures - left Conjugate Gradient, right Quasi-Newton. Find ten differences!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
PS
We will have the symbol of partial derivation in Prime 8.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
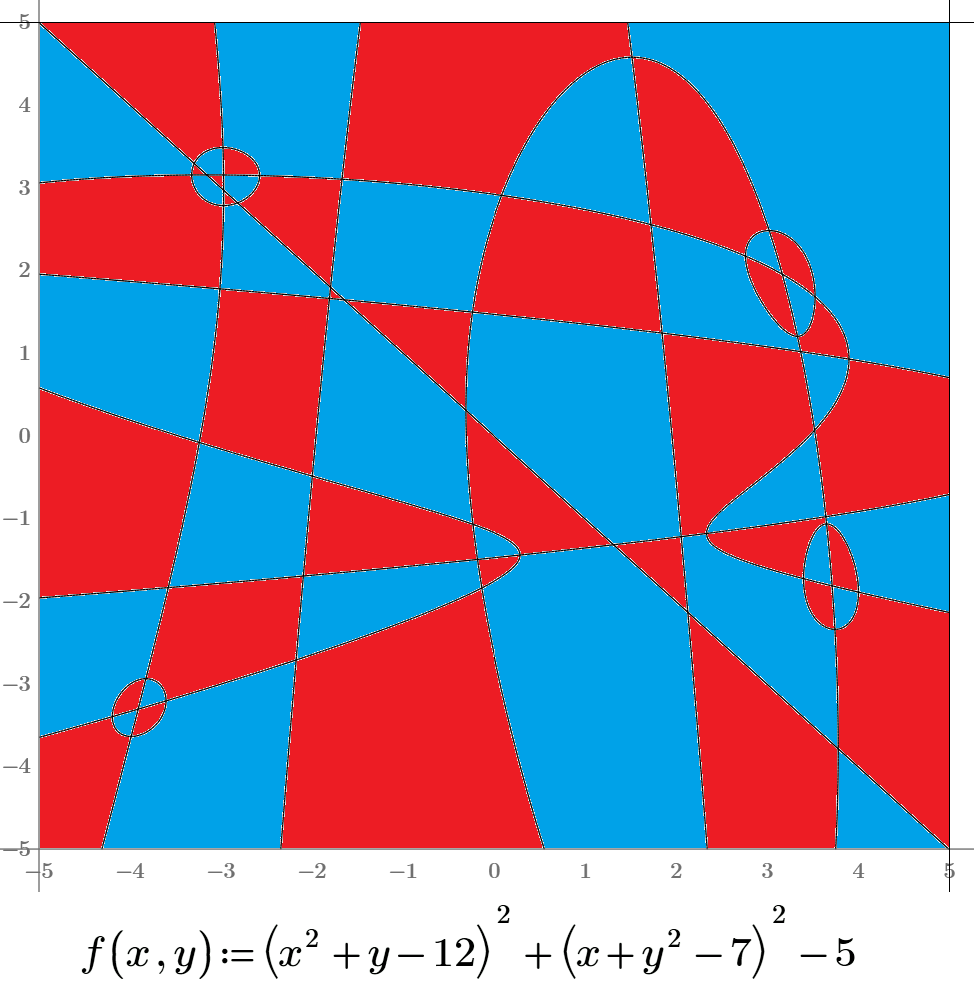
With the function!
Do you know f(x, y) needs more than 2 colors?