Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolic Calculus in MathCAD, are these two limits wrong?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolic Calculus in MathCAD, are these two limits wrong?
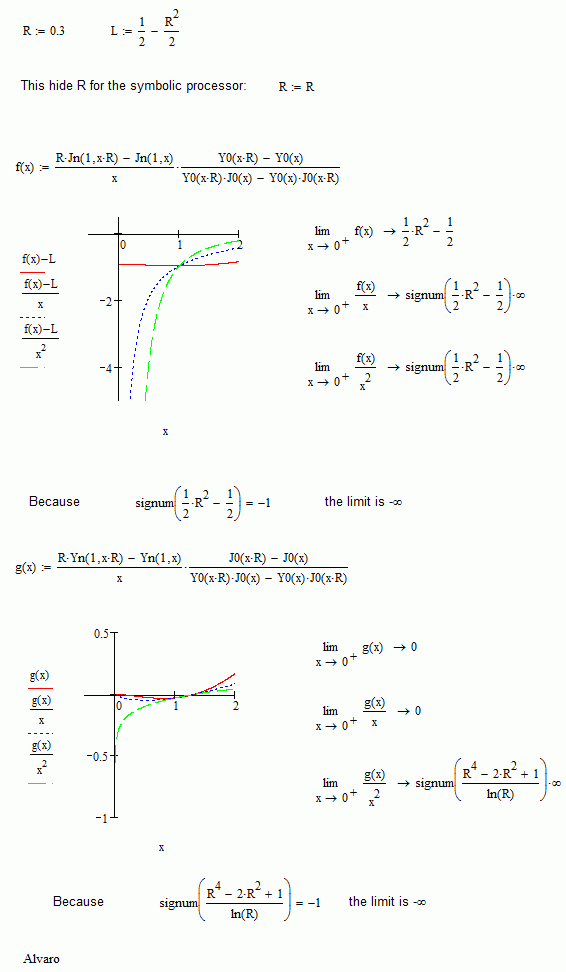
How to calculate Limits with MathCAD symbolically...the series expansion suggest ( at least in one case ) that they should be finite, however the calculus result is infinite...Why? Furthermore it would be possible to calculate the limit without assigning a value to R ( I think not ).
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Massimiliano.
The limit it's a property of the variation of the variable, not for some fix number. So, the best way to "see" it is plotting the variation, or make a table of successive values. If you can prove that the function have not reasons for vary it's behavior, like discontinuities or zeros or discontinuities of the derivative, and have some bound for the variations, can acotate the limit. The theorem about this is that any monotone bound function have a limit, and any monotone unbounded function diverges. The particular value for the limit it's another question, it's more important say that it exist.
The attached is the study for your limits, in mathcad 11, because mupad isn't very good taking limits. Actually the old version of maple within mc11 is bad too, but enough for this case.
Notice also that posting pictures instead of files make more difficult to write an answer.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Massimiliano.
Limits are poorly implemented in mupad. Even that, in your first limit what I see as first impression is ((1/2-ratio^2/2)*1-1/2+ratio^2/2)/x^2 which gives the indetermination 0/0, but seems that the denom x^2 decrease speedily than the zero at the numerator, and the limit is infinity. Same thing about the second limit, but in this case the numerator is negative, so the limits grows to minus infinity. This is: as first impression, limits are ok.
But, applying L'Höpital, for generical ratio, you have:
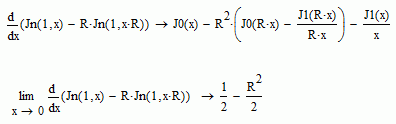
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is what Mathcad 11 (Maple symbolic engine) says:

Further following your steps:

Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi.
Maple take the limits as "undefined" because, by convention, unsigned infinity is undefined in maple. Notice that very simple successions, like n*(-1)^n grows to unsigned infinity, or to both infinity at the same time. This is equivalent to those successions that have limit zero by the two sides, precisely like 1/(n*(-1)^n), the inverse of the previous one. So, this convention isn't very strong, and broke some symmetry about inverses.
But if you take lateral limits, maple now try to found the sign of the infinity, but without much lucky. Eventually, with assume keyword, can make some further simplifications.
BTW both limits by the two sides gives now the infinity answer, but with the sign for determine for some conditions. That's is what is showed in the attached, even the expressions could be horrible: if the limit is plus/minus infinity for both sides, must to be infinity, even the sign could be a more delicate question, and the 'undefinition' of the limit is solved, for instance, for an unsigned infinity, or one with some variable sign, with dependence of the ratio's values. And that's what Massimiliano obtain with Mathcad 15.
This actually is, curiously, for the continuity theorems and the fact that ratio is take as parameter, not a truly variable. If ratio is consider as variable, the problem hold in the 'obscure' theory of bivariate limits.
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alvaro,
Thank you for your clarifications. Now however I am considering the sum of the two previous limits and looks what I found. Is this correct?
Your faithfully,
Massimiliano
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
to better clarify, in the attachment the two limits are calculated symbolically and "evaluated" numerically ( X=10^-17..I think this is the smallest meaningful number ).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Massimiliano.
The limit it's a property of the variation of the variable, not for some fix number. So, the best way to "see" it is plotting the variation, or make a table of successive values. If you can prove that the function have not reasons for vary it's behavior, like discontinuities or zeros or discontinuities of the derivative, and have some bound for the variations, can acotate the limit. The theorem about this is that any monotone bound function have a limit, and any monotone unbounded function diverges. The particular value for the limit it's another question, it's more important say that it exist.
The attached is the study for your limits, in mathcad 11, because mupad isn't very good taking limits. Actually the old version of maple within mc11 is bad too, but enough for this case.
Notice also that posting pictures instead of files make more difficult to write an answer.
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes Alvaro,
Each limit is infinite, but the sum of the two is finite...:) ( I think the sign of L should be the opposite ) and Mathcad could calculate symbolically it!
Best regards,
Massimiliano





