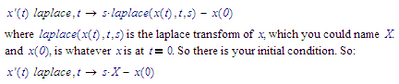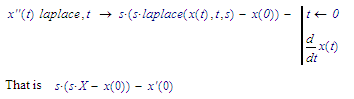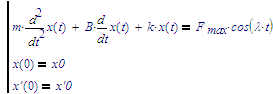Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolic Differential Equations with Initial Symbolic Value
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolic Differential Equations with Initial Symbolic Value
Hi All,
I just figured out how to use prime 6 to solve differential equations both for numerical and symbolic. And if I set the initial value for numerical solving as 0, the results are exactly same with that of symbolic solving. But if I set the initial value for numerical solving not equals 0. The symbolic solving is hard to get the same results.
I learned how to solve differential equations in this video: https://www.youtube.com/watch?v=7xgvPoL_KMg, from 14:00 to 30:00. The examples in this video are based on initial values equal 0.
So could anyone let me know is there a way to solve symbolic differential equations with symbolic initial value?
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You should attach your sheet with an example so we can see which problem you experience.
And ... Prime provides no way to solve a differential equation symbolically in an automatic way! But it may help you solving it manually by using Primes symbolic integration or symbolic Laplace and inverse Laplace transform.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Please see details in the attachment. I used both numerical and symbolic calculation, and drew the time domain curves. We can find the curves are not same. So could I get the same curve using symbolic solving compared to the numerical one?
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Obviously Luc answered your question even before you posted your file 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is because Tim forgot to tell you an important detail.
The laplace transform of the derivative of x(t) is not simply s*X, but it is:
Likewise, the laplace transform of the second derivative of x isn't simply s^2*X, but:
There's your other initial condition.
In Tim's example that doesn't matter, because he had both initial conditions set to 0.
Now, if you name your initial conditions x(0)=x0, and x'(0)=x'0, then the full symbolic solution to the differential equation of the spring system:
should be:
(This expression probably will NOT show, as it is too large to display, it spans several pages).
If you want to take this further, I'll point you to:
- Install Mathcad 15 (as a licensed user of Prime, you can also install and use Mathcad 15 using the very same license file that you used in the installation of Prime)
- check out this item:https://community.ptc.com/t5/PTC-Mathcad/Toolbox-Solving-Ordinary-Differential-Equations-symbolically/m-p/689336#M192090
Success!
Luc