Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolic derivative
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolic derivative
Hello,
I am trying to evaluate the derivative of a function symbolically.
Would anybody, please, help me with this issue?
Best regards,
Sergey
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have to define x(t), that is, use ': ' to get ':=', not set it as a boolean (bold =),.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
before the symbolic derivative you must use clear(A), clear(B), clear(t), clear(omega) or also clear(A,B,t,omega), furthermore you have to use the definition symbol " : " for the function definition and not the equal to "=", as Luc says in his post.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
Thanks for reply.
As long as I can see, it doesn't work.
Would you please use my .mcdx file and apply your suggestion properly?
Sergey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have to define x(t), that is, use ': ' to get ':=', not set it as a boolean (bold =),.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hei,
I used "clear (A)" and then defined "x(t)" as you advised. It worked.
Mathcad's results are complying with my beforehand calculated values.
Thanks a lot.
Best regards,
Sergey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
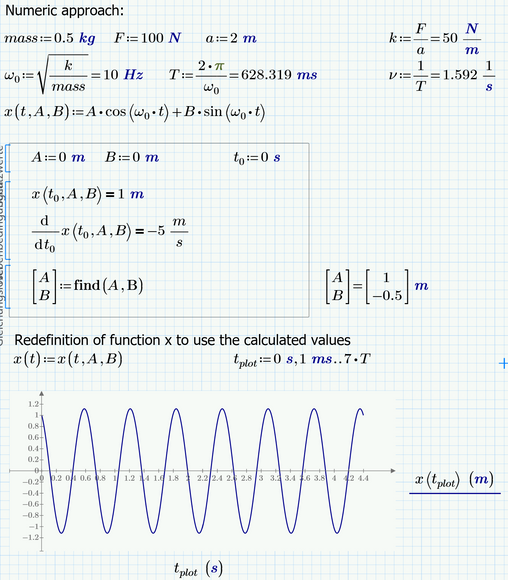
If your goal is to find the derivative but use the value of B you defined and the value of A you found using the solve block, the attached sheet should help.
What had to be changed:
1) B (and possibly x, which later is overwritten by function x) should be defined outside of the solve block
2) no need for x=1 in the solve bock as x IS 1
3) clear variable t (at least for symbolics) - you don't want it to be 0s anymore
4) Make the result of the solve block usable for the symbolics by using the inline evaluation "trick"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sergey uses Prime < 5...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
Sergey uses Prime < 5...
Too bad. Sergey did not mention that.
Here is a pdf printout of the sheet, in case Sergey is still interested.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
Still interested :).
The values of "A" nad "B" are not defined but to be found.
Briefly:
- First I find the value of "A" by applying initial conditions.
- Then after the constant "A" is found, I need to take the derivative of a function symbolically which, in turn, contains the value of "A".
- After that I apply my second initial conditions to find "B".
I attach my lastest version of mathcad file.
If you have any idea of how to make it "easier" or more logically, please, let me know.
Sergey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello again.
I did this task a little bit differently.
Now I have only one question: I have an error message: "This variable is undefined". How do I get reid of it?
Sergey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have cleared it, just above the line where it says it's undefined, in the Clear(A,B,w0).
It does not help if you take the w0 out of the clear statement, beause then Prime will start complaining about A (or B).
Attached is a way.
Note that your way of solving first A then B gets you the same answers for this particular case. It is because your initial condition, at t=0 will make the sin(w0*t) =0, so the value of B doesn't matter, and the cos(w0*t)=1, so the value of w0 doesn't matter either. If your function would be different such that at the initial condition A would still depend on B, and/or w0, then your stepwise approach will fail. Then you will have to solve the equations simultaneosly, as I did as shown above. Or you can put both equations, the one for x(t) AND the one for x'(t), in the solve block, and have Prime find A and B simultaneously...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Lucs symbolic solution in his Prime worksheet does not work for two reasons:
.) Prime does not like the capital "S" in solve
.) Primes auto labelling once again ruined the job. Some of the variable names A, B are labelled differently. If all are labelled the same ("auto" OR "variable") the symbolic solution works OK
In case you wonder why Luc is posting a non-working version: He is using Prime Express and so has not access to advanced features like symbolics, programming, etc. So he has to do the work "blindfolded" which he is able to do because of his huge experience with older (and better) Mathcad versions.
Find attached a Prime 4 worksheet with the working symbolic solution and a slightly different numeric approach using just one single solve block:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, I see it.
Thank you for help and attached file.
Here is my solution (attached) based on all feedbacks, which works for any change in input values.
Do you agree with this solution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You posted just a picture!
You may get rid of the argument omega_0 when defining functions x
you can delete the first and third of your constraints in the solve block as they aren't doing anything
I wont use the temporary variable "constants" but rather replace it with a vector [A,B] as seen in my sheet.
To avoid typos or other errors I'd prefer to define x(t) after the solve block using the original function rather than retyping the function term. Its also seen in my sheet how this works.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I applied proposed changes and it looks good (attached file).
Only one thing remains: I can not get rid of omega when defining the function of x. I get error message.
My goal is to have both symbolical and numerical solutions together which is convenient, in my opinion.
Otherwise it works well.
Sergey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Sergey wrote:
I applied proposed changes and it looks good (attached file).
Only one thing remains: I can not get rid of omega when defining the function of x. I get error message.
My goal is to have both symbolical and numerical solutions together which is convenient, in my opinion.
Otherwise it works well.
Sergey
You have to delete the fourth argument omega in ALL occurrences of x(...)
I have put the definition of t:=0s back inside the solve block as that way after the solve block t still is a free variable. It does not matter, though, as you redefine t as range variable anyway.
AS an alternative you might get rid of t:=0s altogether and use constraints like x(0s,A,B)=1 m, etc. in your solve block. Matter of personal taste I guess.
Worksheet in P4 format attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok. I got it.
I think that we can consider this case closed 🙂
Thank you.
Best regards,
Sergey Dukman