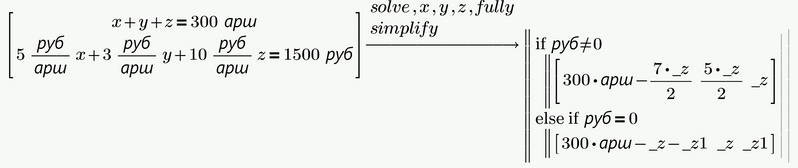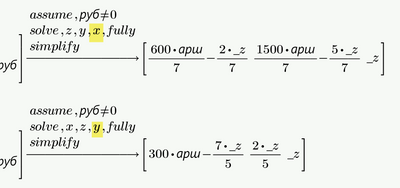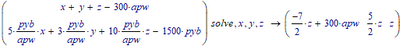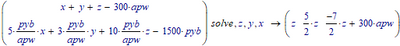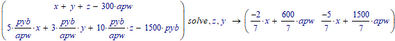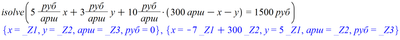Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolic engine of Mathcad 15, Prime and Maple
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolic engine of Mathcad 15, Prime and Maple
Why is the Symbolic engine of Mathcad 15 and Prime so lazy, why should I work for its?
Luc! What about Mathcad 11 with Maple Symbolic engine?


Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
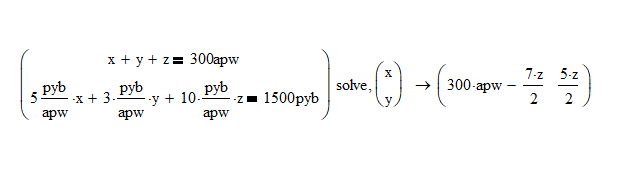
Just solve for x and y with Mathcad Val:
I'm not sure that Maple's z = z is a very useful solution!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Why is the Symbolic engine of Mathcad 15 and Prime so lazy,
lazy??
Is the engine lazy because it does not voluntarily provide all the solutions, or is the user lazy because he only asks for one solution and does not explicitly demand that he want to receive all the solutions? 😄
BTW, the legacy engine (MuPad) in P6 is a bit more precise and also considers the case руб=0
So to achieve the same function as shown above, the user must explicitly state that руб is not zero using "assume"
BTW, you can control which variable the engine uses as parameter by changing the order of the variables after "solve". The name(s) of the parameter always will be _z, _z1, ... ,though.
why should I work for its?
I'm afraid that the question of why you should use Prime and its symbolic engine can only be answered by yourself. I believe no one is forcing you to do this 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just solve for x and y with Mathcad Val:
I'm not sure that Maple's z = z is a very useful solution!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just posted an answer about 20 minutes ago but for reasons unknown to me it had disappeared.
EDIT: Looks like now, after a long time, that first posting of mine is finally showing up. Not sure what was going on.
In short you have to tell Prime that you want to see ALL solutions (don't be lazy 😉 ) by using the modifier "fully".
The "assume" statement is only necessary when using the legacy engine (MuPad) because only this engine correctly considers the case py6=0.
If you want Prime to not use z but another variable as parameter, you simply have to change the order of the variables after "solve". The parameter will still be named _z, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
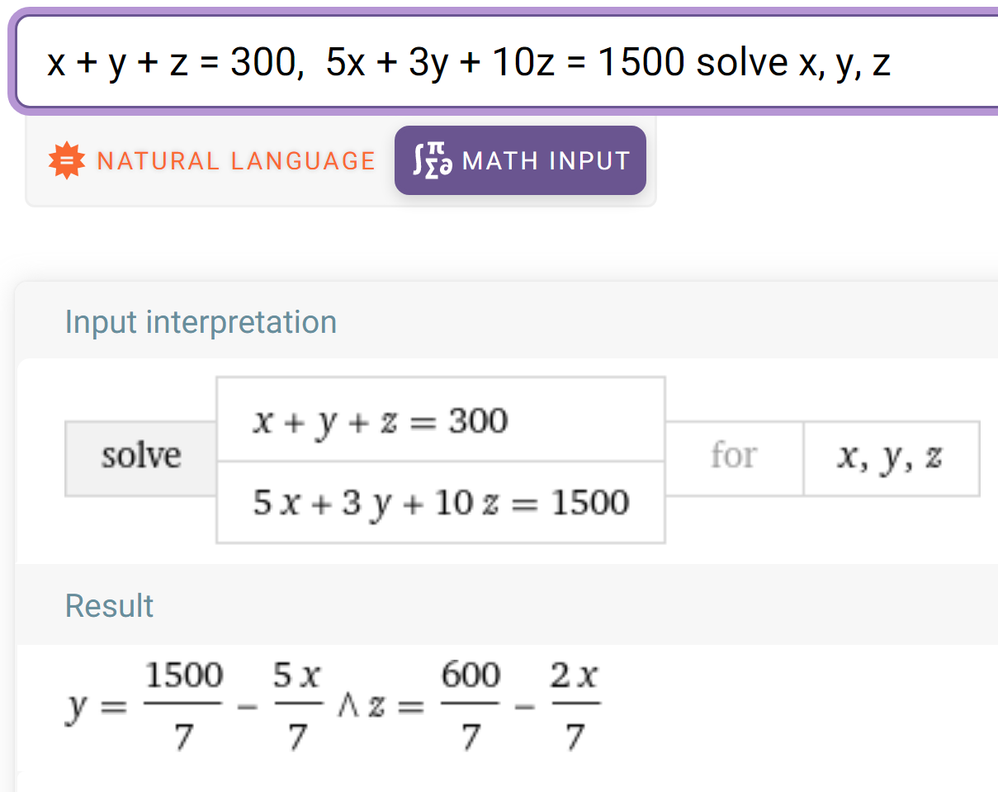
No sure what you want to show with the WA screenshot!???
WolframAlpha uses the first variable stated as parameter (if possible), Prime uses the last one.
Wolfram delivers all solution without asking, Prime delivers just one solution unless asked to provide them all.
BTW you can make the solution dependent on x in Prime, too, if thats what you want. Simply change the order of the variables after "solve".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
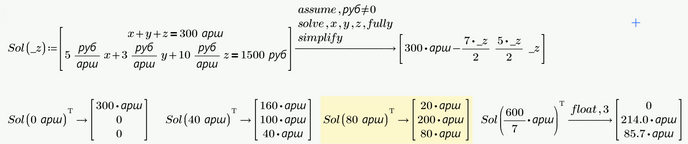
You have (only) two equaltions, and want to solve three parameters, then one of those three is free to choose.
Maple indicates that by setting its value to itself:
Note how the solution for z is z...
The order in the 'solve' directive doesn't matter:
You should specify which is your free parameter by not solving for that parameter, Example, choose x:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is this a Diophantine-type equality? Can you limit the domain to integers?
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Переводите, плейте, прекрасно, рассказ Антона Чехова!
Гимназист VII класса Егор Зиберов милостиво подает Пете Удодову руку. Петя, двенадцатилетний мальчуган в сером костюмчике, пухлый и краснощекий, с маленьким лбом и щетинистыми волосами, расшаркивается и лезет в шкап за тетрадками. Занятие начинается.
Согласно условию, заключенному с отцом Удодовым, Зиберов должен заниматься с Петей по два часа ежедневно, за что и получает шесть рублей в месяц. Готовит он его во II класс гимназии. (В прошлом году он готовил его в I класс, но Петя порезался.)
— Ну-с... — начинает Зиберов, закуривая папиросу. — Вам задано четвертое склонение. Склоняйте фруктус!
Петя начинает склонять.
— Опять вы не выучили! — говорит Зиберов, вставая. — В шестой раз задаю вам четвертое склонение, и вы ни в зуб толконуть! Когда же, наконец, вы начнете учить уроки?
— Опять не выучил? — слышится за дверями кашляющий голос, и в комнату входит Петин папаша, отставной губернский секретарь Удодов. — Опять? Почему же ты не выучил? ты, свинья, свинья! Верите ли, Егор Алексеич? Ведь и вчерась порол!
И, тяжело вздохнув, Удодов садится около сына и засматривает в истрепанного Кюнера. Зиберов начинает экзаменовать Петю при отце. Пусть глупый отец узнает, как глуп его сын! Гимназист входит в экзаменаторский азарт, ненавидит, презирает маленького краснощекого тупицу, готов побить его. Ему даже досадно делается, когда мальчуган отвечает впопад — так опротивел ему этот Петя!
— Вы даже второго склонения не знаете! Не знаете вы и первого! Вот вы как учитесь! Ну, скажите мне, как будет звательный падеж от meus filius?
— От meus filius? Meus filius будет... это будет...
Петя долго глядит в потолок, долго шевелит губами, но не дает ответа.
— А как будет дательный множественного от dea?
— Деабус... филиабус! — отчеканивает Петя.
Старик Удодов одобрительно кивает головой. Гимназист, не ожидавший удачного ответа, чувствует досаду.
— А еще какое существительное имеет в дательном abus? — спрашивает он.
Оказывается, что и «anima — душа» имеет в дательном abus, чего нет в Кюнере.
— Звучный язык латинский! — замечает Удодов. — Алон... трон... бонус... антропос... Премудрость! И всё ведь это нужно! — говорит он со вздохом.
«Мешает, скотина, заниматься... — думает Зиберов. — Сидит над душой тут и надзирает. Терпеть не могу контроля!» — Ну-с, — обращается он к Пете. — К следующему разу по латыни возьмете то же самое. Теперь по арифметике... Берите доску. Какая следующая задача?
Петя плюет на доску и стирает рукавом. Учитель берет задачник и диктует:
— «Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?» Повторите задачу.
Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138.
— Для чего же это вы делите? Постойте! Впрочем, так... продолжайте. Остаток получается? Здесь не может быть остатка. Дайте-ка я разделю!
Зиберов делит, получает 3 с остатком и быстро стирает.
«Странно... — думает он, ероша волосы и краснея. — Как же она решается? Гм!.. Это задача на неопределенные уравнения, а вовсе не арифметическая»...
Учитель глядит в ответы и видит 75 и 63.
«Гм!.. странно... Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то».
— Решайте же! — говорит он Пете.
— Ну, чего думаешь? Задача-то ведь пустяковая! — говорит Удодов Пете. — Экий ты дурак, братец! Решите уж вы ему, Егор Алексеич.
Егор Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет, бледнеет.
— Эта задача, собственно говоря, алгебраическая, — говорит он. — Ее с иксом и игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил... понимаете? Теперь, вот, надо вычесть... понимаете? Или, вот что... Решите мне эту задачу сами к завтраму... Подумайте...
Петя ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из угла в угол.
— И без алгебры решить можно, — говорит Удодов, протягивая руку к счетам и вздыхая. — Вот, извольте видеть...
Он щелкает на счетах, и у него получается 75 и 63, что и нужно было.
— Вот-с... по-нашему, по-неученому.
Учителю становится нестерпимо жутко. С замиранием сердца поглядывает он на часы и видит, что до конца урока остается еще час с четвертью — целая вечность!
— Теперь диктант.
После диктанта — география, за географией — закон божий, потом русский язык, — много на этом свете наук! Но вот, наконец, кончается двухчасовой урок. Зиберов берется за шапку, милостиво подает Пете руку и прощается с Удодовым.
— Не можете ли вы сегодня дать мне немного денег? — просит он робко. — Завтра мне нужно взносить плату за учение. Вы должны мне за шесть месяцев.
— Я? , да, да... — бормочет Удодов, не глядя на Зиберова. — С удовольствием! Только у меня сейчас нету, а я вам через недельку... или через две...
Зиберов соглашается и, надев свои тяжелые, грязные калоши, идет на другой урок.