Symbolic solution of one optimization problem

[ValeryOchkov]

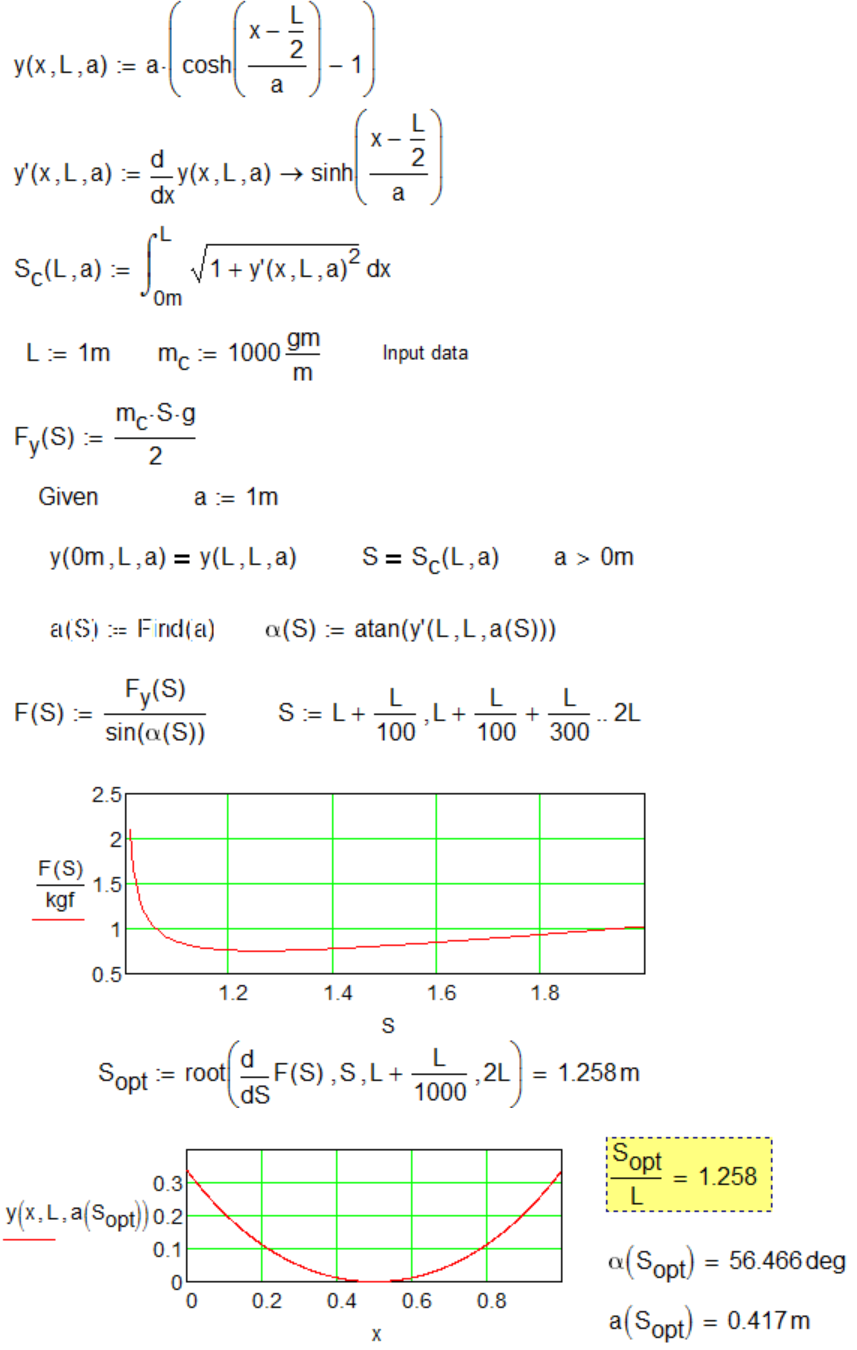
One interesting optimization problem.

Chain attached to two sides of the wall at the same height.

What should be the chain length, to force to the attachment points was minimal?

See below the numerical solution.

Is it possible to full analytical solution?

[ValeryOchkov]

More simple numerical solution in attach (without h):

.

[AlanStevens]

I can't see an analytical solution, but here's a simpler approach to a numerical solution:

Alan

[AlanStevens · Accepted solution]

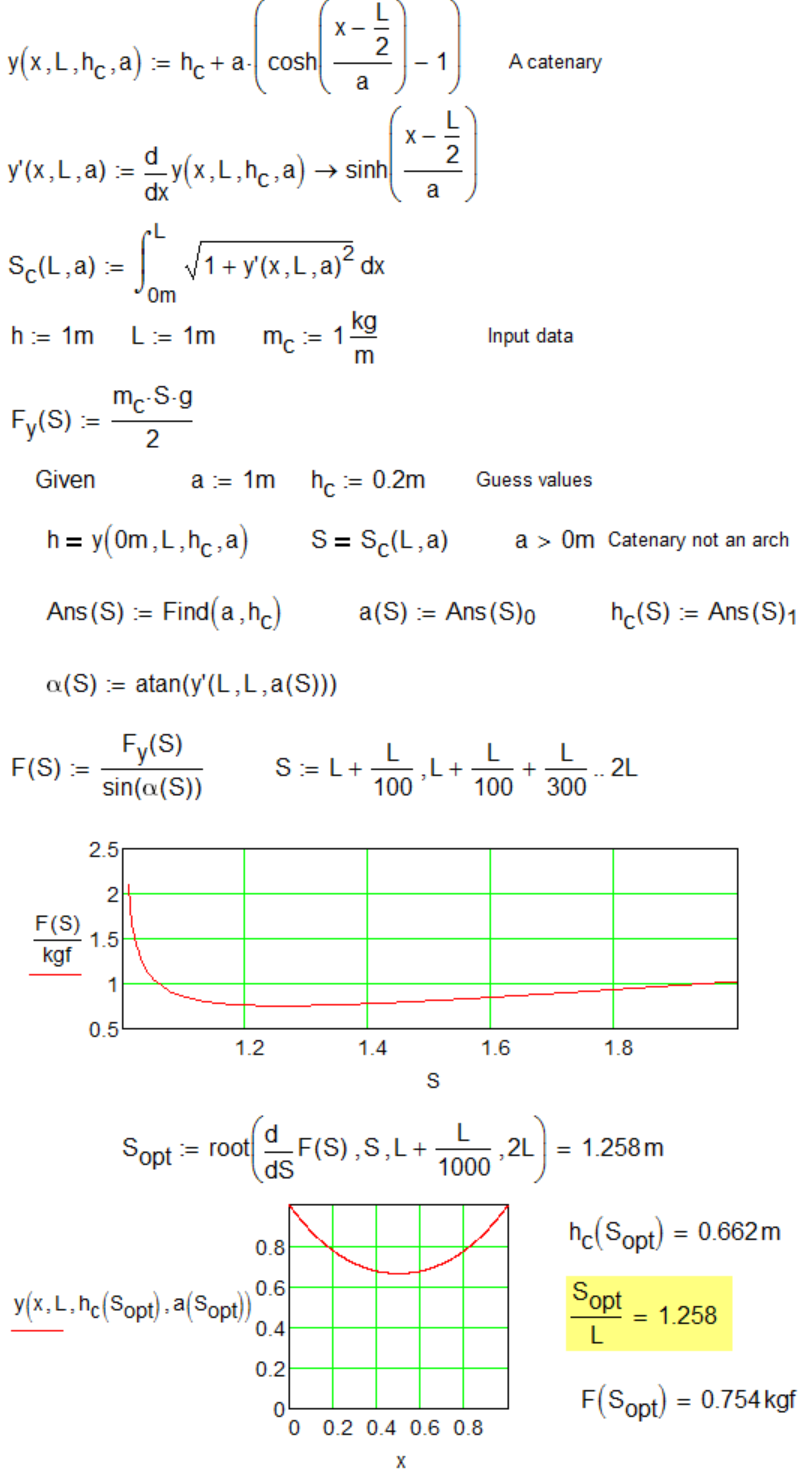
Or even simpler:

Alan.

[ValeryOchkov]

Thanks, Alan!

But I hope to get a symbolic solution!

[AlanStevens]

Valery Ochkov wrote:

Thanks, Alan!

But I hope to get a symbolic solution!

My second solution above is mostly symbolic.  The symbolic procedure breaks down at the point where we seek a solution to tanh(z) = 1/z, where even Mathcad's symbolic solver selects a numerical answer!

Alan

[ValeryOchkov]

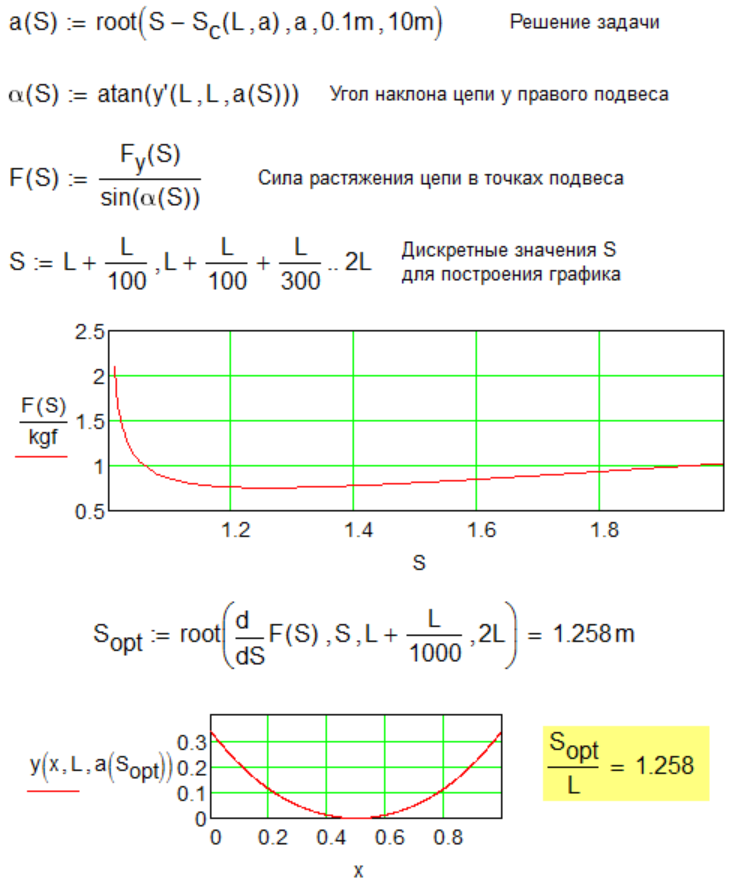
I think the balance between simplify and understanding is so:

Root with 2 argument - no solution

Root with 2 argument - solution

[ValeryOchkov]

And what an optimal value must have a in this canonic formula y=a*cosh(x/a)?

I think it will be one new math constant!

Was this problem studied in past?

[LucMeekes]

Possibly, this is what I get purely symbolically (Note that gravitation and the chain mass per unit of length don't matter.)

You get the answer for the optimum length of the cable expressed in L, the distance of the attachment points:

But you had seen that already.

Luc

[ValeryOchkov]

ValeryOchkov wrote:

Was this problem studied in past?

Yes!

See The optimum spanning catenary cable - Michigan State University - SciVal Experts 4.6

C.Y. Wang

(Profiled Author:  Chang Y Wang) 

European Journal of Physics. 2015;36(2).

Scopus

Full text |

Abstract  © 2015 IOP Publishing Ltd.

A heavy cable spans two points in space. There exists an optimum cable length such that the maximum tension is minimized. If the two end points are at the same level, the optimum length is 1.258 times the distance between the ends. The optimum lengths for end points of different heights are also found.

[ValeryOchkov]

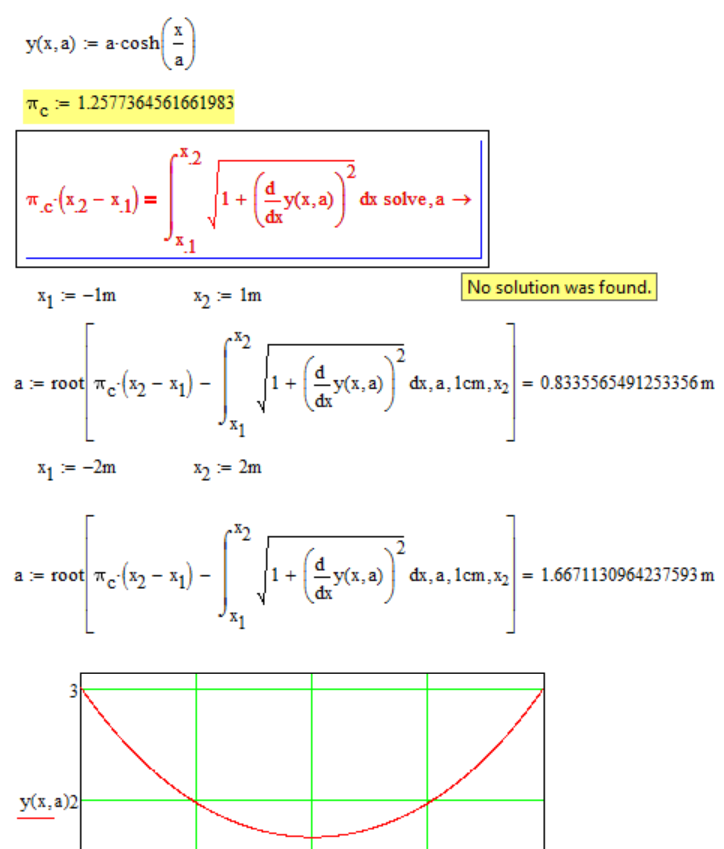
ValeryOchkov wrote:

And what an optimal value must have a in this canonic formula y=a*cosh(x/a)?

It is impossible -

[ValeryOchkov]

ValeryOchkov wrote:

I think it will be one new math constant!

The catenary PI: 1.258...

How many digits can we calculate for this Math constant?

As for the circle PI (3.142...)

[ValeryOchkov]

Please see section 4.8 of

http://www.people.fas.harvard.edu/~sfinch/csolve/erradd.pdf