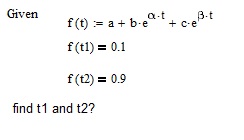Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolic solution to an exponential function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolic solution to an exponential function
Hi All, I have a function which including two exponential components, whose power factor x and y are different. I was trying to solve it by hand or by Mathcad solver, but did not succeed. Would anyone give me the instruction how to do this?
Since an approximated solution is also acceptable, I also tried to use the brute force method, in using match(0.9, XXX) and match(0.1, XXX) to solve, but it seems an exact match cannot be achieved. If someone can teach me how to get the approximated match, that would also be very helpful. Thank you!
Solved! Go to Solution.
- Labels:
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think you will find a symbolic solution. To find a numeric solution you need to define a, b, c, x, and y. You can make the solve block a function of some or all of those parameters if you wish to vary them though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't think you will find a symbolic solution. To find a numeric solution you need to define a, b, c, x, and y. You can make the solve block a function of some or all of those parameters if you wish to vary them though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A symbolic solution is possible for given values of x and y:
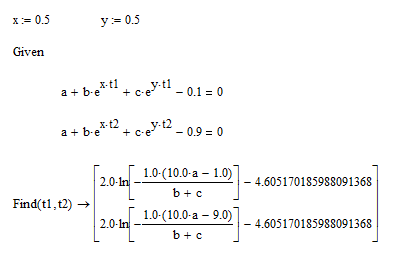
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Richard.
I think that this symbolic solution is only for the particular case that x=y.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It appears you can often obtain a symbolic solution if you know the ratio between x and y:



However, for some ratios, the solution is too large to display:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Mark.
But notice also that there are not a 'true' system of equations, both are independent and can be solved separately. This enable the use of root function.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, you are right. It gets ugly otherwise:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Yhuang.
Symbolically, can't. Numerically, a solution in the attached.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Alvaro!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Would not it be better to propose the problem in this way?