Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolic solve problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolic solve problem
Hi all,
sorry for link rather than attachment. I have been trying to solve (symbolically) a system of equations which, it seems, I can only do using a solve block. The problem is that I want to create a function from the solution so I can re-use it and evaluate numerically. The solve block solution seems only to allow a symbolic evaluation of the result. I could of course cut and paste the symbolic solution into a function but this seems untidy. If I solve a simple system of equations using the solve keyword then I can evaluate both symbolically and numerically, however, the solve keyword method won't solve my real problem.
Please see linked MC11 sheet in which I have started with a very basic problem and then moved on to my real problem. I'm using MC15.
Regards,
Dave.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just noticed your advanced problem - included that in this attachment.
Alan
Worksheet replaced with a neater version - in MC14/15 format..
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You need to supply initial guesses for a and b - see attached.
Alan
PS You can upload files by clicking use advanced editor (top right), then Choose File at bottom of advanced editor.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And if your equations are always linear, you could use lsolve (no initial guesses required):
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm working at home on iPad hence unable to upload. I'll look at your worksheet on Monday.
Many thanks,
Dave.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just noticed your advanced problem - included that in this attachment.
Alan
Worksheet replaced with a neater version - in MC14/15 format..
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How would you use that last version to get a result?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
How would you use that last version to get a result?
Like this?
For example:
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you!
My fault, I was thinking of the symbolic solution to compare with the symbolic solve. Don't think we can get it that easy with the solve block set up that way as MC can't determine the dimensíons of the vectors.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
... I was thinking of the symbolic solution to compare with the symbolic solve. Don't think we can get it that easy with the solve block set up that way as MC can't determine the dimensíons of the vectors.
Correct. I'm afraid I was only thinking of the numerical approach. I had the "solve" version in mind for the symbolic approach.
Both numeric and symbolic approaches work ok if the system is reformulated to work with lsolve:
(The last assignment also works ok if the vector of components on the LHS is simply replaced by s)
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you. Now I realise that the crux of the matter is giving Mathcad enough info to do it's job. The fact that this can be passed in via a function is very useful.
Dave.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You need to supply initial guesses for a and b - see attached.
... or use the symbolic evaluation directly after the "find"
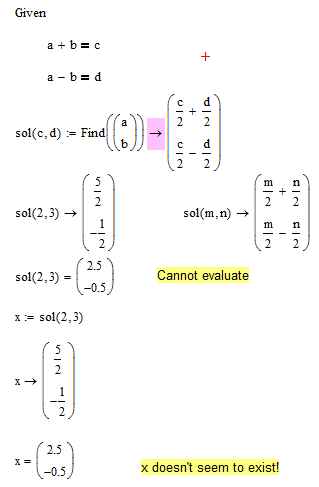
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks,
Why should that have made a difference? Is it simply a quirk of Mathcad or is there a logical explanation of rule for this?
Regards,
Dave
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is it simply a quirk of Mathcad or is there a logical explanation of rule for this?
The latter. An assignment will be affected by the most rightmost expression of the RHS of the assignment if there are some inline evaluations. Look at the example below. To show the difference PI had to be evaluated symbolically as we wouldn't see any difference by numeric evaluation:

In case of the solve block the assignment without the symbolic eval assigns the whole solve block to the function sol(). So every call of sol() evaluates the whole solve block again. This means that evaluating numerically using the normal = sign uses the numerical approx algorithms and requires guess values (and as you don't provide any your sheet fails here). But if you evaluate symbolically different algorithms are chosen which do not require any guess values and so you see a result in your sheet.
The added symbolic eval changes this behaviour as now sol() is not assigned the solve block but rather the result of the symbolic eval which is the 2x1-vector in c and d. Of course this vector can be evaluated numerically, too, without the need of guess values, as long as you provide numeric values for c and d.
This method works only if the solve block can be evaluated symbolically to a simple symbolic expression which may not be the case for some more complex tasks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks,
that was very helpful.





