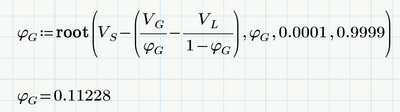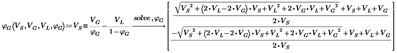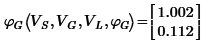- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolic solve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolic solve
A simple equation solved symbolically for an unknown variable returns two results, - as expected.
However I know the result lies in the range 0 - 1.
If I add an 'assume' modifier to limit the result to the value <1, I get quite an unexpected result.
The units are obviously causing all sorts of mayhem.
What's going on here?
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Primes symbolic doesn't know about units and so it can help (and is often necessary) to tell the symbolic engine that the used unit (meter in your case) is real and positive. This is often necessary even if you turn on "Units/Constants in symbolic" in the calculation options and sometimes it doesn't help at all (which is unfortunately also true for the modifier "assume").
But there is no need to use the symbolic "solve" if you are just after one numeric answer - especially if you know the range the solution is to be expected.
You may use a numeric solve block or the "root" function to do the job, the latter being more compact, does not need a guess value if you provide a range and doesn't look that ugly:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
I have mistakes.
UNIT "m" has polarity ?
I think this Is bug.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Primes symbolic doesn't know about units and so it can help (and is often necessary) to tell the symbolic engine that the used unit (meter in your case) is real and positive. This is often necessary even if you turn on "Units/Constants in symbolic" in the calculation options and sometimes it doesn't help at all (which is unfortunately also true for the modifier "assume").
But there is no need to use the symbolic "solve" if you are just after one numeric answer - especially if you know the range the solution is to be expected.
You may use a numeric solve block or the "root" function to do the job, the latter being more compact, does not need a guess value if you provide a range and doesn't look that ugly:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you all for your responses.
My take-away from this is the symbolics don’t like units, and there are other (better) ways of solving for the variable.
Thanks.
Sent from Mail for Windows
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you do want a symbolic result, then you can do as follows:
And a numeric evaluation of that function gives you:
Success!
Luc