Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
System of equations not converging due to exponential term
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
System of equations not converging due to exponential term
Hi, I am trying to solve a system of 3 equation by iteration 'n'. The system of equations is solved over a range 'x'. There is convergence to a solution over a certain part of the range of 'x' but no convergence over the other part. I believe the exponential term in one of the equations is generating a number that is too large for mathcad to handle. Is there any way to get around this problem? Perhaps some reworking of system of equations to modify the exponential term (logarithmic scale)? Or is there another way I could go about solving this system of equations? Thanks, Jon (Please see the attached file)
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If it's the infinite n solution you are actually interested in then a a Given ... Find solve block is probably a better approach - see attached (I've only included the Case 2 values, but it works ok on the Case 1 values, reproducing your large n values of J, deltaC etc.).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What range of x is it not converging over? Your equations all seem to work ok for me (but perhaps you had limited the range). Some of your graphs look like solid colour simply because there are so many lines jumping rapidly between two values. You can overcome this by selecting 'no lines' in the plot trace.
See attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Alan. The solution is not converging over the range of about 0<x<550. I have included a graph for x<550 and for x>550. You will see that in the latter case the solution converges to a single value rather than bouncing. As a result of the values bouncing back and forth, the solution that is being generated is non linear. I have updated the file to show how the solution should behave - linearly. Any help on how to get the solution to converge to a single value over the whole range of x would be very helpful. Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How do you know it's supposed to converge rather than oscillate over that range? I note that you've set one of the C constants to zero - is it meant to be zero in the actual base equations (it certainly runs into numerical problems if set to the order of the other constant!)?
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, C1 is meant to be set at zero, which eliminates the exponential term in the numerator.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When I solve the same system of equations in Matlab the solution converges over the whole range...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
J M wrote:
When I solve the same system of equations in Matlab the solution converges over the whole range...
OK. If it converges in Matlab then it should converge in Mathcad for something so simple. Could you post the Matlab code?
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If it's the infinite n solution you are actually interested in then a a Given ... Find solve block is probably a better approach - see attached (I've only included the Case 2 values, but it works ok on the Case 1 values, reproducing your large n values of J, deltaC etc.).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Alan, This seems to have done the trick!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi, Thank you for all your help. I am hoping to develop the model further now. I want run the model over a range of i, where each successive element i+1 depends on i (finite element analysis). I have tried to develop this (please find it attached) but I think I am way off. Should I be using some kind of loop function? Thanks, JM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Don't know if the attached will help or not! Some values of DeltaC are complex, so there is probably an error somewhere, but the workfile should help point you in the right direction for iterating loops.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Alan, This is really helpful, definately has me on the right track. The results are not what I expected but I'm wondering if that's due to the complex numbers you pointed out. I tried a few things to sort that out (as you'll see in the attachment) but with no luck. The variable of interest is E. E(x) should behave as an inverted parabola over the whole piece-wise range of i. I believe it is the complex numbers that are causing it to behave unexpectedly...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
J M wrote:
I believe it is the complex numbers that are causing it to behave unexpectedly...
Those complex number could be the result of Mathcad being mathematically too exact. As it was already discussed here, Mathcad evaluates (-negative real number)^(1/3) to the complex number with the smallest argument and not to the negative real number (with the argument pi) an engineer probably would expect.
During your iteration the values of Q get negative and therefore the values of Y get complex as of the expresssions (Q..)^(1/3).
Setting AR to 1.5x10^5 instead of 1.5x^10^6 seems to avoid that problem (Q not getting negative) and it looks like you are getting the results you expect. But I think thats not a solution for you as I guess you would have choosen that value for good reason.
I tried forcing Mathcad to return the real,negative value using absolute value and sign operator by replacing the two expressions "(Q..)^(1/3)" with "(|Q..|^(1/3) * sign(Q..)", but then the routine does not evaluate because the solve block throws the error of not finding a solution.
So it looks like the error is either in the values/equations in the sheet or in your expectation 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looks like the problem is the accumulation of small errors in calculating the Q's. See the attached for an alternative way of calculating them.
Also, noting Werner's point about cube roots, I've replaced the Q^(1/3) notation by the n'th root notation. This has the advantage that it crashes if Q goes negative, so you are immediately aware that something is wrong!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Looks like the problem is the accumulation of small errors in calculating the Q's. See the attached for an alternative way of calculating them.
Also, noting Werner's point about cube roots, I've replaced the Q^(1/3) notation by the n'th root notation. This has the advantage that it crashes if Q goes negative, so you are immediately aware that something is wrong!
Alan
I don't yet see that those two ways in calculating the Q's are equivalent, but the definition in your last file is closer to JM's original definition and seems to do the trick pretty well.
BTW, using the n'th root notation won't crash if Q goes negative but returns a real (negative) value and does more neatly the same as my proposed absolute value/sign combination.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
I don't yet see that those two ways in calculating the Q's are equivalent,
You're right! What I did does not match what is in 3c.xmcd. Where I have a difference of two J's in the construction of Qi I should have a sum of J's from 1 to i-1. Unfortunately this also introduces noise into some of the plots! More haste less speed!
BTW, using the n'th root notation won't crash if Q goes negative but returns a real (negative) value and does more neatly the same as my proposed absolute value/sign combination.
I should have been more careful to specify that what I meant was the routine that calculates DeltaC and J crashes.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The graphs and values look quite the same as in you Q3b (slight differences, though)
Should it be of advantage with respect to accuracy to let the solveblock calculalte that factor deltaQ rather than doing it directly as in your Q3b?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Should it be of advantage with respect to accuracy to let the solveblock calculalte that factor deltaQ rather than doing it directly as in your Q3b?
I'm not sure my approach in Q3b is correct as it doesn't really match JM's approach to calculating Q. Q3d is much closer to JM's approach and it looks like the solve block does the calculations more accurately. However, JM might decide it is still not close enough. Just because the graphs are smooth doesn't necessarily mean they are right! I find it difficult to make a judgement call here because I don't know enough about the underlying system being modelled.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As you and Werner say, the expression for finding Q is not equivalent in Q3b. The Q3d is equivalent but for me there is an issue with the solve block because it gives a " " error. To give a little more background which might be helpful. My reference for this model is a Matlab file which I have attached. In addition to converting the model to Mathcad I am also trying to improve it so that a range of x can be considered. In the reference model I have to manually change x (see line 62) in order to compare outputs.
JM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Does the file throw that error (which?) as it was posted or did you change anything?
Alans file (Q3d) works fine for me. I'm using Mathcad 15 M020.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok, sorry about that, I was a little hasty in my reply - Q3d is working fine. The curves seem to behave as expected. A couple of minor things though - I cannot handle the variables Qr, Qs, C1 and C5 (see the plots I attempted in the attached file). Is this because they are not solved in the 'for' loop? Thanks! JM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
J M wrote:
...The curves seem to behave as expected. A couple of minor things though - I cannot handle the variables Qr, Qs, C1 and C5 (see the plots I attempted in the attached file). Is this because they are not solved in the 'for' loop?
They are solved for, they just weren't returned by the routine. They are returned in the attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Alan, I am looking at the results of Qr and Qs over the range of i and it is clear that there is a problem. Qr should linearly decrease from its initial value 10 and Qs should linearly increase from its initital value of 20 (see A3). Instead there is a jump at the begining of the range of i and then the opposite happens. Perhaps the problem is with the deltaQ term introduced in Q3d. I have tried to improve the inital value of deltaQ by changing it from 0 to deltaQideal but that seems to have had no effect (see A4)...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
J M wrote:
...Qr should linearly decrease from its initial value 10 and Qs should linearly increase from its initital value of 20 ....
Now it does! The previous routine incremented Q from i=1 instead of i-1. However, correcting this reintroduced noise! To remove the noise and get the Q's to change in the right direction, the attached routine calculates deltaQ only once per i, based on the average (over x) of J for the previous i iteration. This might be a step too far!!
Alan
(Incidentally, I assume you solved your Matlab problem - line 107, S1 should be S1(x))
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's true, I didn't notice the lack of i-1. But as for the next step, yes, that's one step too far. Each value of x should be treated independantly, so taking the average J[i-1 over the whole range of x defines the problem in a way that is not correct.
Also, in terms of the output while Qr and Qs output now follow the expected curves, S1 and S5 are now incorrect. In 'A4' S1 increased linearly from its initial value of 0, while S5 decreased linearly from its initial value of 30, this is as it should be (see A4). In 'A2d' however S5 now increases from its initial value (see A5). Troubleshooting the numerical methods aspect of this problem is kind of surpassing me...
PS. Thanks for your reply regarding the other post. You were quick because I didn't leave it up for long! I took it down to review a few things. I will be reposting it...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If the problem really is that of an accumulation of small errors, then i don't understand why they show for the lower values of DeltaP!? I have changed back the delta to its original definition (I think). I have left X set to the value you assigned (14000) rather than using the calculated one (15000) as the latter will get the solve block to fail.
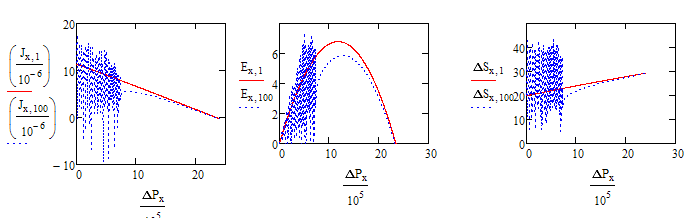
Whats noticeable, too, is, that if the values of TOL and/or CTOL are deceased (from the default 10^-3) the solve block will fail.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have gone back to take a look at what we had with 'Q3' (reposted as B1). It gives just about the same output as what we are getting with the new deltaQ term that was introduced with 'Q3b' (see B3) except that the latter one shows the noise while the former doesn't.
I am not sure where to go from here. In another thread I posted about my attempt to write this same program in Matlab. Do you think that this would be a better bet? Unfortunately I'm even less comfortable in that format than I am with Mathcad. As you can see from the attached Matlab code, this version is just trying to get off the ground (see A2).
Also with regard to my note on the behavior of S5, that is not an issue, this was just a typo, in the solve block the C5 should have had a - deltaC term.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry I guess I can't help but I think I can at least explain the noise in B3 in contrary to B. I seems to make no big difference if the deltaQ is caclulated in the program in the next iteration step as in "B"or if its obtained as solve variable from the solbe block as in "B3". The vital difference is the third root. Regardles of the method some of the Q will get negative. Using the ()^(1/3) notation will get you complex values which makes the calculated outcome complex and can not be plotted, therfore no noise. Using the nth-root notation yields neagtive values which influence the outcome in a way we see as noise and the solve block will fail more often that way.
So the problem remains the weak solve block. Trying to decrease the values of TOL and/or CTOL failed for me and rewriting the first equation (multiplying nominator and denominator by the recoproke first exp term and collecting terms) did not change the behaviour. Don't know if scaling the values would make the solve more stable. Attempting to work on the expressions in the solve block, maybe finding a different approach seems to be the way to go. I guess you already checkd and double checked your equations and constants so I won't advise that.
According to Matlab I am not familiar with - no clue if that could be the better way.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for all your help. I'm going to try to approach the problem from a different angle and perhaps that will help. To limit the complexity I am going to consider just 1 value of x and march that scenario forward through i. I'm posting a new thread with this... Thanks!





