I'm taking Jason Hafner's edX course Waves and Optics https://www.edx.org/node/3261#.VF-6xfnF-So . I've been trying to use Mathcad Prime 3.0 to solve the various problem sets. The ability to control units automatically is a great advantage although sometimes this makes you think hard about making equations dimensionally correct. Recently I tried to solve a problem with the symbolic "series" command. I had mixed success. Here's the problem.
We are taught that any problem f(x) = mass*d2x/d2t has a hidden form -k*x = mass*d2x/d2t which is Newton's Law for Simple Harmonic Motion (SHM) of a spring. If f(x) is non-linear, i.e., it has terms like x^2, e^x or sin(x), we can linearize it close to an equilibrium point using the Taylor's series for f(x). For SMH problems the equilibrium point is usually taken at xeq where f(xeq) = 0.
To linearize we are interested in only the first two terms of the Taylor's series:
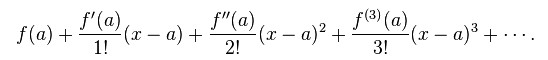
Since f(a) should equal zero, and 1! = 1, we are really interested in only f ' (a) * (x - a) , and we hope all of the remaining terms represent a negligible error.
The problem in Mathcad is that you get instead of f(xeq) = 0,
and if you try to use symbolic "series" command to get the Taylor's series for f(x) you get a horrendous numerical expression of little use. I gave up on the "series" command.
I found it easier just to compute f ' (xeq) . That's all you need. Then the desired angular frequency is sqrt((f ' (xeq))/mass) in garbage notation.
