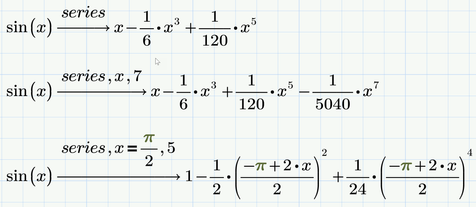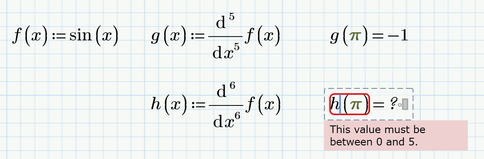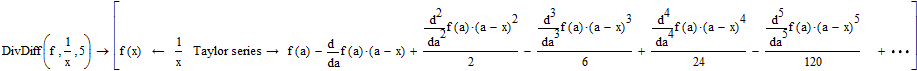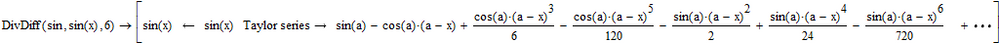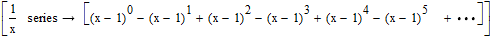Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Taylor series not working
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Taylor series not working
Hi everyone,
Taylor's serial development doesn't want to work. Attached is the error displayed. Thanks in advance for helping me solve this problem.
Thank you.
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its hard to debug a picture, so you sure should attach your worksheet.
Is this the only command you experience problems with or are the errors with other symbolic commands, too?
Only thing that I notice is that Prime should detect "sin" as being a function and should therefore display it in non-italic letters. Can it be that you redefined "sin" somewhere above by writing something like sin:=123 ? This would make sin a variable. But this should result in a meaningful error message (like "this must be a function").
Have you tried to close Prime, create a new fresh sheet and type the expression from scratch?
After all, here is what it should look like:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello, Attached is the file. There is only the sine function. Not every function works with Taylor expansion.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just as an exercise (since I'm using Prime Express and symbolics are premium) I tried to create a Taylor Series numerical evaluation function. And, SURPRISE, it worked (at least a little.) For whatever reason, you can only have the first five derivatives (a six term expansion.)
It works on sine function. It does truly strange things to 1/x.
Attached Prime 4.0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
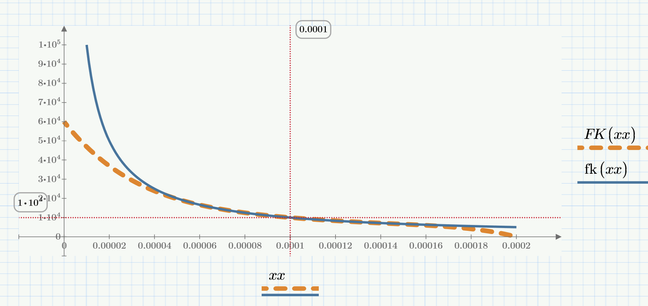
It works on sine function. It does truly strange things to 1/x.
Not so strange if you consider the range of convergence and chose an appropriate zoom:
The numerical Prime limitation to just five derivatives is indeed strange:
But the Prime help at least is not hiding that limitation. Its states: "The derivative and prime operators do not compute derivatives of order greater than five. However, you can nest derivative operators within each other to compute higher order derivatives, with associated loss in accuracy for each successive order."
So there may be a workaround using successive nested derivative operators. Not sure if it could be done without programming in Express. I just tried and the derivative operator dos not accept a function like ceil(i/2) at the placeholder for the order of the derivative. The idea was to nest the ceil(i/2) derivative and the trunc(i/2) derivative to allow in a first step up to the tenth derivative.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your quick response, Taylor's development is well known. For the function 1 / x is not defined in x = 0, it is normal we cannot apply the expansion to around x = 0. My problem is that I don't understand why the Series command won't work.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Taylor's development is well known. For the function 1 / x is not defined in x = 0,
Thats the reason why Fred did the development around x=0.0001 🙂
And the series expansion is valid only for 0 < x <0.0002
My problem is that I don't understand why the Series command won't work.
So why don't you answer my questions and why don't you attach a failing worksheet so we can judge if there is something wrong with the sheet or your installation of Prime?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator