- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Total Beginner Confusion
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Total Beginner Confusion
Dear All
OK, I'm a bit nervous about landing on PlanetPTC, so I thought I'd explain why I've come here to ask for help.
I'm a 68 year old metallurgical engineer, recently retired. That's at least three reasons why I need a bit of help. I don't do TwitBook or any of this new fangled social networking stuff in case I forget that quite a few engineers, most of them with exceptional engineering skills, have aspergic tendancies and can't communicate very well. In order to avoid both further softening of the brain, and daytime television (well actually any televison at all), I've started to look at a few projects from my past where I was a little uneasy about the result. This is the challenge. Engineers will know what I'm talking about: management in too much of a hurry, not enough resources to follow up the oddball result, a hunch that something doesn't smell right, intuition interacting with experience, etc.
I first touched a computer keyboard in 1964, and did a bit of programming up to the early '70's - anyone remember Elliot Autocode or Algol? - and some statistics, and have used spreadsheets extensively: SuperCalc, Quattro Pro and lately Excel. However, I've never used spread sheets solvers, which I think are actually optimisers a la Cox & Box (ICI Monographs on Statistical Techniques in Research & Production, Oliver & Boyd, mid 1950's). This was some 30 years before Taguichi's application of statistics to work at Ford in the 1980's
I do not like to pigeon hole people, but it is possible that metallurgists, particularly industrial metallurgists, aren't particularly good at maths and in particular, not very good at matrices, matrix algebra, and matrix solutions to get an answer. After all, if you pick up a book on matrix algebra, you will find it crammed with subscripts and superscripts, but very short on applications. I would include myself in this pigeon hole .
As possibly the original interdisciplinary discipline, metallurgical engineers might be concerned with metal physics (density of vacancies affecting the ageing of their aluminium alloys or the toughness of their tempered martensite compared with the core tougness in case hardened steels); chemistry (stress corrosion cracking of stainless steels, trace element influences on turbine superalloy properties); the intracacies of welding, brazing and soldering; not to mention sheet metal metallurgy, extrusion, forging and all the process stuff - can we get enough strain rate on the 12000 ton hydraulic press to drive the dynamic recrystalisation far enough, and thus achieve the properties we want, especially in the leg of this undercarriage forging? This is only one side: the other side is understanding the engineers' designs, stressing, etc., to select the right material for the job. In other words, it is complex enough without this peripheral matrix stuff and the manipulations that go with it.
I came across Mathcad recently, and have access to Version 14, and even a manual to read before I go to sleep. I'm not making very good progress, but I am getting to sleep very quickly. As a suggestion to help people like myself, could I ask if there is anywhere a decent glossary of Mathcad terms. For example what is a solve block?
The first problem I've started on concerns the interference fit of an inner member (a 'pin') into an outer member (a 'sleeve'). I won't bore you with the metallurgical details, but at the time this project was hot, I wanted to examine the stress state of the pin and sleeve including the effects of the interference fit. The only half competent engineer in the company who could do this had recently fallen down stairs and was recovering in hospital (steel stairway, 2 storeys = broken ribs, arm and leg), and mangement vetoed taking the job into hospital to reduce his boredom or the hire of temporary outside help. So the analysis was never done, and the solution implemented depended heavily on experience and luck. The analytical stress solution involves Lame's equations for thick cylinders.
The first problem I have run in to is that one cannot do anything, apparently, without having defined variables and even values to those variables. In many ways, this is similar to Excel. Lame's equations contain two mysterious 'constants', A & B, which are a combination of material properties and the specifics of the particular geometry one is attempting to analyse.
The solution methodolagy I am trying to implement is as follows:
1. List and enumerate the material properties and units to be used.
2. List and enumerate the geometry
3. Derive required intermediate values from known geometry
4. Start with the equation for the circumferential stress in the sleeve at the interface between sleeve and pin, see attached worksheet. This gives the stress in terms of the interfacial pressure P. I apologise for the talky nature of this sheet, it is just that hopeful of obtaining a solution, I've added notes as an aide memoire for future use.
5. State the equations for circumferental and radial stress components in the pin. You have two equations with four unknowns: the two stress components, plus constants A & B.
6. Look at the boundary conditions for the circumferential stress in the pin. One boundary is the bore of the pin where P is known to be zero, so you have an equation with A & B only as unknowns. The other boundary condition is at the interface between the pin and the sleeve, and here you have an equation for P in terms of A & B unknown, because P here is the same as the P in step 4.
7. Find A & B in terms of P by solving the simulataneous equations.
8. Find the circumferential stress at the interface on the pin side of the interface with P as the major unknown.
9. Thus, at the common radius (the interface) we know the circumferential stress on both sides of the interface. We can now compute the strains on both sides of the interface, again in terms of P.
10. But we know how the components were originally machined, so we know both the nominal interference fit, that is the amount by which the pin outer diameter is greater than the sleeve inner diameter. And this must equal the sum of the strain on both sides of the interface. So we can compute the interface pressure P. Furthermore, we also know the tolerances on the original machined dimensions so we can do a tolerance stack analysis and see how this affects the stress situation.
11. Knowing the interface pressure P, we can compute the constants A' & B' for the outer sleeve.
12. Knowing P, A, B, A' & B', we can then compute the the circumferential and radial stresses at any radius in both members.
I very much want to discover how to use Mathcad, so I need somebody in the community who is prepared to work with me (slowly!) step by step to overcome the detailed errors I will undoubtedly make at each step. I do not feel getting the solution in a single piece of advice would make me a better user. What I feel I am missing is (a) an understanding of the background philosophy embodied in the product (this might help avoid errors of the 'undefined variable' type) and (b) where it is appropriate to use the matrix facilities and symbolic capability to produce an answer.
For example, I suspect that a matrix plus symbolic solution can be used in step 7. But I cannot get anywhere near there because of the anomalous error message I get in the sheet, concerning the constant B. Here the sheet, at the second instance of the constant B, tells me it is an undefined variable. Why not at the first instance? And yes it is undefined, or more accurately unvalued, because this is what I am trying to discover by solving for it. It is like an error message in Algol where you used a variable in computation which was not declared at the head of the program as a variable. But Mathcad appears to have no way of declaring a variable without having a value attached to it.
Finally, are there any books that are recommended as (a) application desriptions of Mathcad in mechanical engineering and (b) an introduction to matrix solutions in engineering. Perhaps titles like: Mathcad for Metallurgists, or Engineering Applications of Matrix Techniques for Metallurgists would fit the bill or perhaps Mathcad and Matrix techniques for Dummies would be better.
And now I have got to the end, how does one attach a worksheet to a message?
Kind regards
John Smith
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When Mathcad sees an equation that has a := in it, it assumes the equation is either a formula with input parameters or a variable that requires immediate evaluation.
If A and B are defined (using A:= and B:=), then Mathcad can evaluate C:= A + B.
If A and B are not previously defined, the equation must have the form C(A,B):=A + B, and so on. Otherwise, you will get an error (red letter).
For instance, your first equation should be re-written as sigma_c(A,B,r):=... And so on.
If you want to simply write a formula like C:= A + B but not have Mathcad try to evaluate it, right click on the equation and select "Disable Evaluation". You can always turn that back on.
Also, I think your first equation (sigma_c:=...) is corrupted for some reason. If it doesn't work for you, you'll want to delete that equation and re-do it.
I'm not big on symbolics, so I can't be of much use there.
Also, under the "Help" menu, select "Tutorials", which should be useful in getting up to speed quickly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
MichaelH
Thanks for your quick response.
I have actually tried a few of the tutorials. If I have missed the point you have made about the form of equations in them, then I'll put it down to old age, otherwise this rather basic point is not in them.
Onwards and upwards!
Kind regards
John Smith
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello!
Some useful resources from PTC for getting started with Mathcad:
1) On “LearningExchange” are available some video tutorial: http://learningexchange.ptc.com/tutorials/by_product/product_id:4;
2) "Demos & Tech Tips": http://www.ptc.com/products/tutorials/mathcad.htm;
3) Some videos are available on "PTCstudio" channel: http://www.youtube.com/playlist?list=PLF56308229AA2E115&feature=plcp;
3) "Engineering Resources - Powered by Mathcad" (Mathcad worksheets and video tutorial): http://www.ptc.com/appserver/search/mathcad.jsp
I also recommend to you a book by Brent Maxfield "Engineering with Mathcad":
http://www.amazon.com/Engineering-Mathcad-Create-Organize-Calculations/dp/0750667028
and you can read it this book online here: http://books.google.ru/books?id=DfVVkGnzIJAC&printsec=frontcover&hl=ru#v=onepage&q&f=false
Earlier the e-book (for Mathcad) "Machine Design and Analysis" was available from PTC's site. I attached contents (in PDF format) of chapters "Machine Design and Analysis" and "Metalworking" if you will be interesting any subject/task let me know and I will upload Mathcad worksheet for specific task.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I've set up a solve block to find the values for your problem. (Check "Help" for numeric solve blocks. Also check for functions.) Are you sure that cimferential stress (not radial stress) at the inner and outer surfaces is zero? I would have thought that radial stress at free surfaces was zero.
Second file attached is an excerpt from Roark Handbook, thick cylinder, internal pressure (AKA your sleeve.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One ready-cooked meal.
The "Flywheel . . .Lame.Stresses B radial" file is your original file with my solve block added. I've taken the liberty of correcting your boundary value constraints:
- The radial stress is the stress that matches pressure, not the circumferential stress. So the radial stress at the inside and outside are set equal to zero; the radial stresses at the interface are equal and opposite in sign. Circumferential stress is allowed to wander at will.
The "thick cylinder" sheet is the same as the one I posted yesterday with the dimensions of your sleeve inserted. Note that both the radial and circumferential stresses from both sheets are the same. (This gives me confidence--a seperate, independent check!)
One last note: At least for "shrink fits," the interface stresses are going to be affected by the levels of initial interference. I'm kind of surprised that we didn't have to balance strains to get this solution.
Good Luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
I think your intuition is correct. Even for the same material, you must have E somewhere to get stress from strain, or visa versa. The solutions in your sheets are independent of E and u.
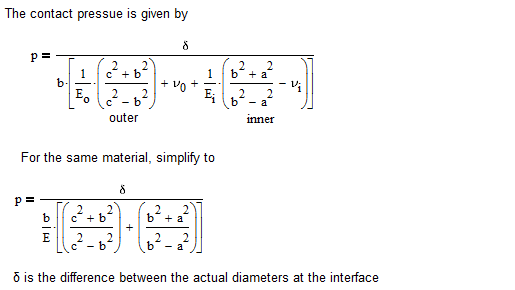
The contact stress is given by the following (no need for a solve block)