Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Transient heat conduction problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Transient heat conduction problem
Hi all,
I am working on a problem for my class and I'm having trouble even beginning to program this transient heat conduction problem.
I have attached a sheet with information regarding the problem I am trying to solve. What I want to do is eventually increase the order of my interpolation functions (from linear to quadratic and so on) and also increase the number of elements I use and compare how well each of these methods converge, but I don't know how to incorporate iterating through time into my dependent variable while still keeping it a 2x1 vector.
Basically, I have a boundary condition at u1 for all timesteps and and an initial condition at t=0 for all x, but short of adding another index onto my u vector, I don't know how to actually iterate through a number-of-timesteps value. I don't think I can add another index onto the u vector because then that would change the outcome when I multiply my matrices by that vector.
The difference scheme I want to use (in terms of variable names in my sheet) is:
[K.hat] * {u}(s+1) = [K.bar] * {u}(s) + 1/4*{Q}(s+1) + 1/4{Q}(s)
Where s is the time step value.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
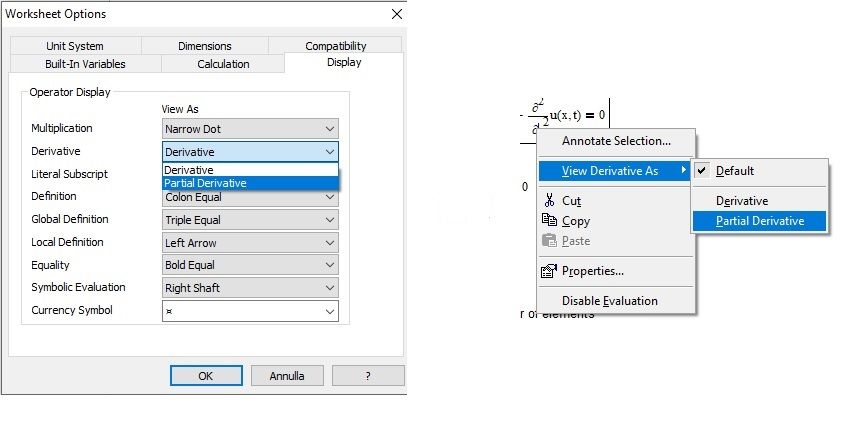
Hi,
Please note that Mathcad offers the "Pdesolve" operator for partial differential equations with some examples. Obviously it is not suitable for educational purposes. To be clearer you should write in the worksheet the difference scheme indicated in the text. Finally, I let you know, for your correctness in writing the differential equations, that there are the following two options to write the simple and the partial derivatives: