Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Units in roman
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Units in roman
Units in roman
I challenge anyone to find a scientific paper or a book in any science or engineering discipline, published by a reputable company, in which units are shown in italics. Please let me know if you find one! In state-of-the-art publishing, units are printed in roman (upright and not bold).
“The International System of Units”, now adopted throughout the world, specifies which units to use and how to write them. Defined in the SI Brochure , it is clear on the subject:
Chapter 5: Writing unit symbols and names, and expressing the values of quantities
Unit symbols
Unit symbols are printed in roman (upright) type regardless of the type used in the surrounding text. They are printed in lower-case letters unless they are derived from a proper name, in which case the first letter is a capital letter.
The National Institute of Standards and Technology (NIST), an agency of the U.S. Department of Commerce, has published “The NIST Guide for the use of the International System of Units”, which is also clear on the subject:
Chapter 6. Rules and Style Conventions for Printing and Using Units
6.1.1 Typeface
Unit symbols are printed in roman (upright) type regardless of the type used in the surrounding text. (See also Sec. 10.2 and Secs. 10.2.1 to 10.2.4.)
where Sections 10.2 and 10.2.1 to 10.2.4 restate and explain the rule.
Essentially, units are written in roman in order to distinguish them from variables which are written in italics. For example, "m" is a variable whereas "m" is a unit. Please refer to one of the above publications for more details. Note that the color of the font for units (as well as for numbers, variables, etc.) is not addressed in these documents..
In Mathcad, displaying units in a color different than that of variables is a good way to distinguish them even better. However, displaying them in italics is unnecessary and wrong.
Mathcad default setting
All the marketing for PTC Mathcad is done with the units shown in bold blue jazzy italics and the product is delivered with this font set by default.
When asked why the default font for units is such, PTC Mathcad dodges the question by saying that, in Mathcad, names of units are treated as variables, so if variables are in italics so should be the units, and that anyways users can easily change the font for units.
The problem
The problem is that my students, who use Mathcad, could think that the default font for units is correct, whereas actually it is wrong and unacceptable.
I have to ask my students to change the font to roman. If they ask me, I can only explain to them that the funny default font was probably a request from the company’s marketing department.
Correcting the situation
There are laws behind the recommended use of the SI units in the U.S. and other countries around the world. Standards are intended to ensure public safety and to improve efficiency in commerce, heath system and teaching. Non-compliance can result in large economic losses. Students are entitled to be taught properly. A court could consider that PTC Mathcad has mislead its users, thousands of students and companies, in thinking that the proper font for units is italics.
While a lawsuit against PTC Mathcad is unlikely, but possible, the company should set a good example and correct the situation by doing the following:
- Clarify the distinction between fonts for units and for variables.
- Change the factory default setting of the font for units to roman (upright and not bold). Colors are fine.
- Modify all advertising to show units in the way described above.
- Publish a white paper announcing the change and saying how great the company is for complying with state-of-the-art publishing and the worldwide SI standard.
References
The “SI Brochure” is available in English at http://www.bipm.org/en/publications/si-brochure/.
“The NIST Guide for the use of the International System of Units” is available at http://www.nist.gov/pml/pubs/sp811/.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the chance that a lawsuit would go anywhere is nil.
You never know what a court would decide.
PTC has not mislead anyone
Rephrase if you like to read "Because the default font for units is italics, users delude themselves into thinking that the proper font for units is italics."
they have not claimed that their font for units complies with any particular standard.
Well,
it would be better if Mathcad adhered to recognized standards
and then they could claim that they do.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Agreed.
You could also add the ISO 80000-1 (Quantities and Units - Part 1: General), which probably takes precedence over the NIST Guide in most countries (I note that the given version of sp811 is dated 2008, and still refers primarily to the ISO 31 series, which the ISO 80000 series replaces).
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I understand your concerns. Please emphasize this point to your students, and require them to adjust their Mathcad documents to correct the problem.
But note that they can adjust Mathcad to correct this problem.
With all that's deficient in the newer versions of Mathcad (which is still a large step backwards from the capabilities in version 15), please don't ask PTC to divert effort to fixing this problem.
This is an opportunity for your students to learn a valuable life lesson: Sometimes you must rework the tool to do what you need. (You can find, in this web site, a long running discussion about showing the equation, then the equation with values, then the final answer. And you can track the torturous path thru the years while we tried to enable this. Mathcad 15 can come closer than Prime, but it still is an elusive goal. And more teaching professionals want to see that from their students than are worried about the font choice for units.)
Styles and standards change. Perhaps we should petition the standard writers to require units be in italics, bold, and blue. 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred Kohlhepp wrote:
I understand your concerns. Please emphasize this point to your students, and require them to adjust their Mathcad documents to correct the problem.
But note that they can adjust Mathcad to correct this problem.
With all that's deficient in the newer versions of Mathcad (which is still a large step backwards from the capabilities in version 15), please don't ask PTC to divert effort to fixing this problem.
This is an opportunity for your students to learn a valuable life lesson: Sometimes you must rework the tool to do what you need. (You can find, in this web site, a long running discussion about showing the equation, then the equation with values, then the final answer. And you can track the torturous path thru the years while we tried to enable this. Mathcad 15 can come closer than Prime, but it still is an elusive goal. And more teaching professionals want to see that from their students than are worried about the font choice for units.)
Styles and standards change. Perhaps we should petition the standard writers to require units be in italics, bold, and blue. 😉
If it were a complicated change, I might agree that it should be low on the priority list. However, as one of Mathcad's major selling points is its unit handling and the changes are simple enough that they shouldn't take even a summer intern too long to design, implement and document, PTC really ought to get it right for the next major release at the very least.
Styles and standards change.
True, but these particular standards have been around a long time (decades) and are fairly well entrenched in the scientific domain. If they change, then it will only likely be after an extensive consultation period and with several years warning. This should give some opportunity for people to postpone learning their valuable life lesson 😉
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
please don't ask PTC to divert effort to fixing this problem.
How much effort would only my request no. 2 require on your part?
- Modify the factory default setting of the font for units to roman (upright, not bold, blue color).
If the amount of work is reasonable, could we settle by considering just this request as a feasible and satisfactory solution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dominique Bauer wrote:
please don't ask PTC to divert effort to fixing this problem.
How much effort would only my request no. 2 require on your part?
- Modify the factory default setting of the font for units to roman (upright, not bold, blue color).
If the amount of work is reasonable, could we settle by considering just this request as a feasible and satisfactory solution?
Effort on my part? Absolutely none, I don't work for PTC.
It took me about three minutes, however, to change the font designation in a sheet and save it as a template.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I agree that it would be better if Mathcad adhered to recognized standards, but the chance that a lawsuit would go anywhere is nil. PTC has not mislead anyone, because (as far as I know) they have not claimed that their font for units complies with any particular standard.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the chance that a lawsuit would go anywhere is nil.
You never know what a court would decide.
PTC has not mislead anyone
Rephrase if you like to read "Because the default font for units is italics, users delude themselves into thinking that the proper font for units is italics."
they have not claimed that their font for units complies with any particular standard.
Well,
it would be better if Mathcad adhered to recognized standards
and then they could claim that they do.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the chance that a lawsuit would go anywhere is nil.
You never know what a court would decide.
I am not a lawyer, but in very obvious cases such as this even if I can't know what a court would decide then I can know what is likely that it would decide. If you prefer, "the chance that a lawsuit would go anywhere is miniscule"
PTC has not mislead anyone
Rephrase if you like to read "Because the default font for units is italics, users delude themselves into thinking that the proper font for units is italics."
Rephrase it any way you wish, as long as it's accurate. The key point in your new version is that "users delude themselves". PTC has not claimed that the font they use conforms with any particular standard, so if users "delude themselves" into thinking it represents some standard then that is the user's problem, not PTC's.
There are other standards for math notation that PTC does not conform to (e.g. notation for scalars vs vectors vs matrices). Also standards for physics, chemistry, engineering, etc. There is no law that requires them to conform to such standards, so as long as they do not claim that they do, you have no case.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
.... The key point in your new version is that "users delude themselves". PTC has not claimed that the font they use conforms with any particular standard, so if users "delude themselves" into thinking it represents some standard then that is the user's problem, not PTC's.
I think it's possibly fair to say that PTC have a part in creating the delusion in the mind of the users, however:
PTC Mathcad provides a complete set of units in the International System (SI), United States Customary System (USCS), and Centimeter Gram Second (CGS) unit systems. You can multiply values by these built-in units or by your own user-defined units. Tables, plots, matrices, and math regions take units. Most built-in functions take units when it is logical. For example, you can add units to a data set and find its average value using the mean built-in function, but you cannot calculate the sine of 2kg. In PTC Mathcad, all variables are displayed in the unit system of the worksheet. For example, to measure the volume of a sheet of aluminum foil, you can define its width to be 30cm, its length to be 1m, and its thickness to be 10μm. When you evaluate each of these variables, the result is 0.3m, 1m, and 0.00001m respectively in the SI unit system. You can then calculate the volume of the sheet without concern about the units of the variables, the result is 0.003L.
Whilst a lawyer might argue that this refers only to the actual units, there is also the (at least implied) claim that Mathcad will conform to the SI itself in its calculations. The unwary user, having read the SI, might also expect "complete" and "displayed in the unit system" to extend to the unit notation.
The text quoted above, however, should give the user some pause as to how well PTC know the SI (or the SP811) as there is no space between any of the quantity numerical values and their corresponding units. A summary execution offence if ever there were one!
.. but you cannot calculate the sine of 2kg.
I disagree ... must get round to writing up it up one day ...
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think that interpreting "PTC Mathcad provides a complete set of units in the International System (SI)" to mean that it implements every recommendation in the SI brochure is a real stretch.
I agree that it would be better if Mathcad complied with the standards. In fact, I would go so far as to say that when Prime was designed it was really sloppy work on someones part to come up with italics for units. I just find it very hard to imagine that any court would take a lawsuit over this seriously.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh, I agree that it would stand remarkably little chance of succeding (at least in English and Scottish law, not sure about USA - seems to be almost watertight compared to some of the law suits I've read about ![]() ).
).
I also agree that somebody at PTC should have got it right in the first place - they must surely have looked at a copy of the SI/ISO/NIST SP?
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Prime (3.1) it is easy to change the font of the unit symbol to non-italic, but I fully agree that it should have been upright from the start.
There IS a space between the value and the unit, see L=15 m below, and that is the only option for ISO 80000-1.

However it only appears in the evaluation, when the cursor is away; not in the definition. I think that may be a breach. In Mathcad (no Prime) there was an option to choose a space for the multiplication symbol, haven't found it in Prime yet.
Note that ISO 80000-1 allows no space (if it does not lead to confusion mN <=> Nm for newton metre), a space an x or a half-height dot for a combination (multiplication) of units, Prime uses the half-height dot (the T=1 kg*m example).
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes wrote:
There IS a space between the value and the unit...
Yes!
Therefore, you may want to discuss the philosophical meaning of the "sine of 2 kg", but not that of the "sine of 2kg". Even Google's spell checker catches that!
Until the issue of calculating sin(2 kg) is clarified, we can assume that sin(2 kg) must have some meaning in SmurfLand and we are reassured by the fact that Mathcad is provided to all with the Smurf notation by default.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
.. but you cannot calculate the sine of 2kg.
I disagree ... must get round to writing up it up one day ...
Hi Stuart,
Ah, the misunderstandings and bad groundings of Quantity Calculus.
Unfortunately, Quantity Calculus, as it is promolgated makes the error of splitting the arithmatic from the 'dimensions' (note I said arithmatic rathers than mathematics;-). This wrenches the whole units, dimensions and scalings away from being a well defined and integrated system.
http://web.ist.utl.pt/ist12219/data/60.pdf Two alternative derivations of Bridgman’s theorem, Mario N. Berberan-Santos and Lionello Pogliani, Journal of Mathematical Chemistry 26 (1999) 255–261
The very idea that a measurement is a pure number to which later is added (in a side by side manner) a reference unit, and even later that the unit can have a scale factor and then some base dimensional multipliers (still side by side, rather than integraal to the measure) is the real source of the problem. "Back in the day" before modern computing, it was the norm to be able to take these (then simple) factors separately, but once complicated functions get in the way that separation fails (bad maths), but the inertia keeps on.
As an aside, have you noticed that mathematicians abstract away all ideas of SI units and Dimenions into their rather conceptual world, but at the same time the very first thing they tell (hammer home; "I'll learn you") all students that all angle must be in radians, a unit without dimensions anyway (and it can be 'added' to quatities measured in Nepers, see any exponential fn)
Further interest http://www.eecs.berkeley.edu/~joschu/docs/history-of-units.pdf shows (but doesn't comment on) how they never even thought about whether angles could be a Dimension (which can't be added to mass or length etc). It's a nice paper though.
regards
Philip
Long live Quantity Algebra for the computer age.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The following is an excerpt from the “International System of Units”:
1.1 Quantities and units
The value of a quantity is generally expressed as the product of a number and a unit. The unit is simply a particular example of the quantity concerned which is used as a reference, and the number is the ratio of the value of the quantity to the unit.
The last phrase could read as: "and the number is the number of units that gives the value of the quantity."
For example, the value of a length may be expressed in the form x = 3 m = 9.84 ft, where m and ft are alternative units for obtaining the same value of the length.
Quantity: x or length
Value of the quantity: 3 m
Unit, i.e. a particular value of the quantity used as a reference : m (m is usually regarded as a base unit)
Number of units: 3
Hence, the value of the length is ‘3 times a meter’ or ‘9.84 times a foot’.
___
The value of a speed v may be expressed in the form v = 25 m/s = 90 km/h, where m/s and km/h are alternative units for obtaining the same value of the speed.
Quantity: v or speed
Value of the quantity: 4 m/s
Unit, i.e. a particular value of the quantity used as a reference: m/s (m/s is usually regarded as a derived unit)
Number of units: 4
The value of the speed is ’25 times a meter per second’ or ’90 times a kilometer per hour’.
___
In Solid Mechanics, also called Strength of Materials, a strain is the measure of a change in length measured over a reference length. The value of a strain espilon may be expressed in the form espilon = 0.005 m/m = 0.005 in/in = 0.005.
The fact that the derived unit m/m is the ratio of two units of the same kind, i.e. units of length, makes strain a dimensionless value. Although ‘strain’ is not a SI units, it is common to use it to indicate that the quantity is a strain. For example, "espilon = 0.005 strain" or more often "espilon = 5000 μstrain" (i.e. microstrain). Note that μ is the prefix micro = 10-6 and therefore is written in roman. (SI Brochure, Section 3.1)
___
A geometric plane angle, simply called an angle, is ratio of the length of a circular arc to its radius. Similarly to the unit of a strain, the unit of an angle is the ratio of two units of the same kind, i.e. units of length (although one is measured along an arc and the other is measured along a radius), which makes angle a dimensionless value.
Because angles are such a common quantity, its dimensionless derived unit m/m = 1 is given the special name radian, where radian is equal to the ratio of 1 m measured along a circular arc to its radius that is 1 m long.
___
Obviously a strain and an angle are two different quantities even if they both happen to have the same derived unit, in this case m/m = 1 called a dimensionless derived unit.
See the “The International System of Units” for more on this subject.
___
I think that mathematicians are more concerned about numbers and the mechanics of counting, calculating, differentiating, etc., whereas physicists and engineers are concerned about quantities, i.e. numbers and units. This is not self-contradictory.
___
Back to the main point of this thread.
I was hoping that someone at PTC Mathcad would say something like: “Dear Dominique, You may have a point. We will consider your suggestion and may modify the factory default setting of the font for units to roman (upright, not bold, blue color) in the next release of Mathcad." ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dominique Bauer wrote:
A geometric plane angle, simply called an angle, is ratio of the length of a circular arc to its radius. Similarly to the unit of a strain, the unit of an angle is the ratio of two units of the same kind, i.e. units of length (although one is measured along an arc and the other is measured along a radius), which makes angle a dimensionless value.
No it's not. That may be how we determine it's numerical value in radians (assuming we measure both lengths in the same unit), but angle is not simply a ratio - as is common with many other quantities, there is no way to distingush quantities of the same dimension from each other, yet even a five-year old can recognize an angle realize that it's not quite the same thing as saying two lengths are different. To my mind, the official definition is putting the cart before the horse or chicken before the egg. And therein lies the heart of the problem. We have a history of using things like trig functions in a dimensionless fashion and, being both institutionally lazy and reactionary, this means that we are loath to change, or even think about changing, all of our nice equations to be correct under an assumption of angle being a distinct dimension.
Dominique Bauer wrote:
Back to the main point of this thread.
I was hoping that someone at PTC Mathcad would say something like: “Dear Dominique, You may have a point. We will consider your suggestion and may modify the factory default setting of the font for units to roman (upright, not bold, blue color) in the next release of Mathcad."
I see Canada still produces some great stand-up comedians! .... ![]()
(
"Units" are just one of many long-standing point-of-debate amongst Mathcad users:
Re: Additional Units for Mathcad Prime 3.0
Re: Additional Units for Mathcad Prime 3.0
As is ISO naming/style adherence:
)
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As an aside, I discoverd a paper on the history of units,
http://people.eecs.berkeley.edu/~joschu/docs/history-of-units.pdf which I found pretty good.
I've emailed John, but it's not a published work, however he said:
> Hi Philip, thanks for your interest in my paper, I'm glad to hear that it was useful.
> It was written for a course I took at Caltech on the history of science, taught by Jed Buchwald.
> I don't have any plans to publish it, as I've moved onto other things.
So grab a copy while you can.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I discoverd a paper on the history of units,
http://people.eecs.berkeley.edu/~joschu/docs/history-of-units.pdf which I found pretty good.
he said:
> I don't have any plans to publish it, as I've moved onto other things.
So grab a copy while you can.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff a écrit:
No it's not. That may be how we determine it's numerical value in radians (assuming we measure both lengths in the same unit), but angle is not simply a ratio - as is common with many other quantities, there is no way to distinguish quantities of the same dimension from each other, yet even a five-year old can recognize an angle realize that it's not quite the same thing as saying two lengths are different.
You are right, I should have written "A geometric plane angle, simply called an angle, is usually measured by mathematicians as the ratio of the length of a circular arc to its radius" or something like that.
It would be like saying that the area of a rectangle 'is' the product of its base by its height. The unit of areas is usually expressed in terms of the SI base units as m2, but it could be expressed in any other way you want. For example, if you take a body in the shape of a rectangular cuboid (a simple example) and if you know its height, its mass and the mass density of the material it is made of, you can easily determine the value of its base area by dividing the mass by the mass density to find the volume, and then divide the volume by the height to finally get the area of the base. That is not to say that the base area of the cuboid 'is' the mass divided by the mass density, divided by length, but that its value could be expressed in terms of (kg/(kg/m3)/m.
On the other hand, if the entire universe was composed only of cuboids, it might be more practical to express the unit for their base area in terms of a more direct function of their mass. But that unit would not correspond to our usual systems of units. In Smurfland, the unit for areas is simply the 'smurf area unit'.
So an area is a quantity, it is not a m2, and you can use different units in order to specify its value, for example m2, mm2, in2, (kg/(kg/m3)/m, smurf area unit, etc., any of which can be converted to the other one.
Same with angles. An angle is a quantity, it is not a radian. Its value can be expressed in terms of radians, m/m, no unit, degrees, turns, grads, 1, etc. A radian is not a m/m either, it is simply equivalent to 1 m/m by definition, or 57.3o, etc.
Of course, an angle is not a dimensionless quantity. The quantity chosen in the SI unit system is the radian (rad). In terms of the SI 'base' units, rad converts to m/m which cancels to 1. Note (b) of Table 3 in the SI document states:
..., but the symbol for the derived unit one (1) is generally omitted in specifying the values of dimensionless quantities.
Well, an angle is a so-called 'dimensionless' quantity only when its unit is expressed in terms of the other SI units. And, quite honestly, I think that the 'rad' symbol or 'm/m' should not be omitted in general.
In the SI system, the unit of a force is the Newton (N), which is equivalent to m kg s-1 when expressed in the SI 'base' units. In just the same way that N is kept for forces and not automatically converted and displayed as m kg s-1, I totally agree with you that Mathcad users should be allowed to keep radian (rad), as well as m/m, as a unit for angles.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
... as is common with many other quantities, there is no way to distinguish quantities of the same dimension from each other...
Yes and no. It is not because some quantities have a dimensionless SI unit, that they are harder to distinguish.
As I mentioned before, strain is a quantity usually expressed using the dimensionless unit m/m =1. Note that it is the unit that is dimensionless, not the quantity. The slenderness of a long prismatic object, such a structural steel column, is measured as the ratio of its height to the radius of gyration of its cross section. The unit corresponding to this measurement is also usually m/m =1.
The fact that angles, strains and slendernesses can be expressed using the same unit does not mean that they are the same quantities. People dealing with angles should consider themselves lucky because angles have their own official 'SI coherent derived unit', namely the radian with its symbol rad. And that's in addition to other units such as degree, rad, turn or revolution, etc. What more could you ask for?
Strain does not have its own special unit. I came up with 'strain' in a previous example (espilon = 5000 μstrain) but it is not an official unit, although it is used in the Test & Measurement industry with the simple definition of strain = 1 m/m. Slenderness does not have any special unit. We could make up one right now, say the sl (for slenderness).
Thus rad, strain and sl are different units for different quantities, in pretty much the same way that kg and m are different units for different quantities. Note that rad, strain and sl have the same SI unit of m/m = 1 just because of the choice of the seven base units in the SI system (m, kg, s, A, K, mol, cd). In the Smurf system of units, which is totally different than ours, rad, strain and sl in fact have been defined as base units.
A volume is usually measured in m3 and so is the first moment of an area. Obviously, they are different quantities. These quantities do not have their own special unit, and both are usually expressed in m3 without much confusion. A torque or a twisting moment and a bending moment, which are not quite exactly the same quantities, are usually expressed in N m, and so is energy, work and amount of heat, although these have their own special unit, the joule (J). Just because moment and energy can both be expressed in N m, does not mean that they are the same quantities. That does not create much confusion either.
Having said all that, the radian (rad) is an official 'SI coherent derived unit' (see the 'International System of Units' document) just as much as the hetz, the newton, the pascal, the joule, the watt, the coulomb, the volt, etc. It is too bad that the unit for angles was not named after a great scientist. Maybe then it would have had a more honorable place in the math class and in Mathcad.
Well then, should the radian be renamed? What about an euclid (Eu), a muir (Mu) or even a scientist smurf (ssf)? Let the mathematicians decide!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think Stuart's point was not that the quantities are not different, but rather that the SI unit system, and the unit system in Mathcad, does not distinguish between them.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
I think Stuart's point was not that the quantities are not different, but rather that the SI unit system, and the unit system in Mathcad, does not distinguish between them.
Yes.
However, (the SI Hit Squad not withstanding), I believe that many things like angles, the problem with gauge v absolute unit problem in Re: problem with units, etc, can be dealt with by adequately handled within the normal "units" framework, by defining one's own System of Quantities & System of Units in accordance with the International Vocabulary of Metrology (VIM). Provided there is a conversion from the user SoQ/SoU to the ISQ/ISU along with any result in User units, it should even be possible to publish results in the User SoU.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
Dominique Bauer wrote:
A geometric plane angle, simply called an angle, is ratio of the length of a circular arc to its radius. Similarly to the unit of a strain, the unit of an angle is the ratio of two units of the same kind, i.e. units of length (although one is measured along an arc and the other is measured along a radius), which makes angle a dimensionless value.
No it's not. That may be how we determine it's numerical value in radians (assuming we measure both lengths in the same unit), but angle is not simply a ratio - as is common with many other quantities, there is no way to distingush quantities of the same dimension from each other, yet even a five-year old can recognize an angle realize that it's not quite the same thing as saying two lengths are different.
I just want to point out a couple of things (as I see them).
First, there is/should be a distinction between a ratio of two distinct measurements, and the scale value of a single measure in terms of its unit of measure (the former is the case for the notional Angle determination where the two lengths are of a different type - straight vs arc).
The second is the distinction between the measurement of a concrete Quantity, especially in terms of a unit of measure that has a base unit (e.g. meeasure a radius in metres), and the abstract basis of that measurement, which is it's Dimension, e.g. Length. The latter is conceptual and is an unknowable multiplier, which would be the part that moves us from 'calculus' to 'algebra'.
The part that is still missing (but is implied elsewhere) is that the list of Dimensions should be extendable such that, for example, a probabilty can't be added to an angle, which is subtracted from a monetary value (Oh, it is already a Mathcad dimension - Oops), with a signal gain added. All of which are said to be 'dimensionless' ratios, but are quantaties that could carry a distinct dimension for the detection and reduction of user error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Philip. And all.
First: Angles are not the quotient of segments, nor it's rate. That a new (sic) technique to measure them. Quotient it's an algebraic operations, and angles (and segments) have nothing to do with math at the level of elemental things, like those that a 5 years old human can recognize as distinguishable "things".
Second: Also, angles are not dimensionless, have a dimension.
Lets to fundament that. Angles are geometrical entities, so, we must to define angles in therms of geometrical elements, probably some very primitive ones: Plane angles are the intersection of two coplanar half-planes. where a halfplane is defined by "primitive concepts", which have no definition, as they figure in the Euclid's axioms, which we take as "true". Planes, points, lines are primitive concepts. Spatial angles are the intersection of two half-spaces. So, there are not distances in this definition, and, obviously, no units yet.
In the attached page, from "Geometría métrica", of Puig Adams, spanish mathematician, and the book that I use at high school, you can read the definitions for "magnitud" and "cantidad" (quantity), and angles and lengths as magnitude examples. Notice that "métrica" came from μέτρον (metron) which means "measure".
So, every set that meets properties 1 to 4, they elements define a magnitude. It's posible to prove that angles verify properties 1 to 4. But we now have a complicate set of theoretical elements. How can take the "angles" from it? That's important, and not specified in the only one book page: by a "representant" of his class. The situation is similar with Q, the set of the fractions, We have a lot of candidates for represent 5/2 = 10/4 = 15/6 = .... But take only one, definid by the property of that div(num,den)=1. So, that's the quantity: those elements that have the same amount (cantidad) of this magnitude.
Note also that mass can be defined meeting this 4 properties too, from m=F/a, where the force and the acceleration can be measures by the elongation of a spring, and acceleration measuring times and lengths. For check that mass are well defined, must to prove that this relation verifies properties 1 to 4.
In that procedure there are no place for the Higg's boson. Also, for times, we can use pendulums. For measuring angles we don't need segments, actually we need half planes, but it's more easy consider the half-lines, defined by a line, a point over the line, and a orientation. The border of an angle, are the set of two half lines. (Border as a topological operator, represented by δ, and actually have a lot of simulates with the mathematical derivative operator). Notice also that in the referred book, the word for the "angle" quantity is "amplitud", which is the measure for the defined magnitude.
Once we have the magnitude, we can let now to see which units we want to use. For example, we can divide the circle into 360 "sectors" (that's the correct name for the circle "parts"), by purely geometrical procedure, without any calculus, and compare that with the "amplitude" of a particular angle, to measure it.
Or can use length of segments to measure angles. But remembering always that angles have nothing to do with the math quotient operation. That's like the Pythagoras theorem: in geometry you don't squaring numbers, but take the geometrical square built over the sides of the triangle.
Some few final considerations, if the reader if not enough convinced. Angles and sides, point and lines, and other couples for space, are dual elements: can be interchanged at any geometric statement (theorem, property or axiom). So, at each statement that mentions length and magnitude, you can interchange it with angles and get reamains magnitude. See Duality (projective geometry) - Wikipedia, the free encyclopedia . For that, they can take as Generalized coordinates - Wikipedia, the free encyclopedia .
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alvaro,
I think you misunderstood my position. I'm all for Angles being a distinct formal Dimension, and have been for a long time. My initial point was a summary of how I see anglular measures (in radians) being currently defined.
My other point concerned how we (are instructed to) do the calculations, which is where I diagree with Stuart regarding his 'sin 12 kg' comment. With an Algebra we can check if the method produces sensible (within its axioms) results. Stuart (I think) would argue that the current Quantity Calculus procedures would allow "sin(12kg)" to produuce a valid result. Just because it's a rule doesn't (in my mind) make it 'right', hence the need for an algebra (or meta algebra) that would allow that computaion to be analysed to see how the consitencies/incositencies pan out, along with how well it meets any purpose that's been identified (another discussion!)
The example is further confused because it confounds point 1 and 2 (angular trig functions, and units pass through), which is then even further confounded by the pure maths vs experimental physics / engineering prediction abstraction/concreteness division.
It all gets very messy.
(for the record, I'd like mathcad's computer algebra system to be able to carry through user-defined dimensions, and that it should have, a-priori, an Angle dimension that can be enabled as a pre-requite for trig & exp(i.theta) functions - see my Beyond the Money Dimension - May09.doc and stackexchange comments. However long experience has indicated that it is good to dream..... but don't get your hopes up too much)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Philip.
My wrong. By two excuses: First, You post was the last when I post mine, so the "answer" was to you. Even I don't like the new definition for angle, just because isn't one, it's only a measure technique, new (sic) one, I know very well your position about angles, and agree with you on it from a long time ago. Actually, some of your old post about angles and units make me to re-study this point.
Second, and as excuse to, I write "Second, Also ...", but want to write, "Second, and as Philip say ..." or something like this, but stop with also, which is very short.
So, I don't refuses your points, because I agree with them, except, (always there are some but) with the correct definition process for some measure of angles, but this is a minor point, just about how to define an angle.
About the sin, or cosine functions, one can take different path: geometry, as segment projection, analytic, as functional properties (from the definition of the exponential as the function that holds f(a*b) = f(a)*f(b) and then use the Euler relations to introduce sin and cos), calculus, as the solution of some diff equation, or limit for some series, and a big etc.
So, for saying that sin(2 kg) make sense or not, must to say for which definition is that. For real numbers, one can prove that almost of the usual definitions for sin gives the "same" function, but remember that the extension for complexes, as an example, defined by sin(z)=(e^iz-e^-iz)/2 it's only a convention. Identify the vertical projection with the sine function was a convention too, derived of the representation of real numbers in a line. For example as what I'm saying, try to represent the sine function if you represent reals as the unidimensional position in a Peano curve, which cover a plane region.
But for make this conventions, at least, there are some considerations, for example, can ask for some coherence. If sin(2 kg) have sense, in the functional definition for sin, you have this:
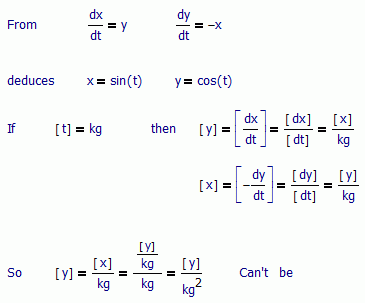
So, with this definition of sin, cos, can't take kg as argument. With this definition, you must to use some unit where [t]^2 = 1. Oh, [rad]^2 = 1:
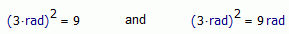
What convenient!
So, also agree with you that could be very difficult to use sin, log nor exp with some other unit, or dimension than a angle.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
so, also agree with you that could be very difficult to use sin, log nor exp with some other unit, or dimension than a angle.
It would be possible, in the Mathcad environment, to set some options that allow some choice for the trig/exp fns about requiring units and whether it's permissive or not. I included those in my Beyond the Money Dimension - May09.doc paper.
PS Can you actually see that paper - do folk need to be logged in to see it, or is it hidden behind some privacy setting?
On the subject of exp(i.theta), the thing is that it's a mapping from the straight line onto the circle, or if it's a (rho+i.theta) i.e. complex, then a mapping (wrapping) of the 2d plane around in a 'Chinese fan' style. Hence the angle/radian part, but also we get that the rho value should be in Nepers, which arguably is a different Dimension (Bone?, as in Napier's Bones;-). Do notice that the dimensional analysis is still correct that you can't and an angle to a bone, as evidenced by the '+' symbol still being there, along with the 'i', the whole thing is almost like a polynomial equation. The '+' meaning 'listed together', rather than actually being capable of summation!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes Philip, anyone visiting the community, without being logged in, can see it.
At least, I can, without being logged in..
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Luc.





