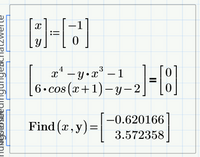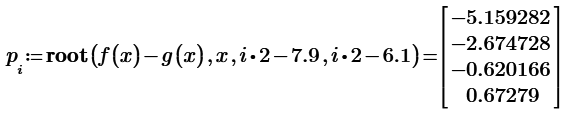Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Using Mathcad to solve a system of non-linear equations using Newton's method
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using Mathcad to solve a system of non-linear equations using Newton's method
Hello,
I am struggling in implementing a problem that implements Newton's method to solve a system of two non-linear equations:
𝑥^4−𝑦𝑥^3=1
6cos(𝑥+1)−𝑦=2
I am trying to implement
𝑥^(𝑛+1)=𝑥^(𝑛)−𝐽(𝑥(𝑛))−1∙𝐹(𝑥^(𝑛))with 𝐽(𝑥^(𝑛))^−1is the evaluation of the inverse of the Jacobian matrix and 𝐹(𝑥(𝑛))is the output of the equations.
I have done most of the iteration work I believe in the function but I am stuck on how to manipulate the values to come up with the intersection points of these two functions.
Here is my code:
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you are just looking for a solution, you sure would use Primes built-in methods ("root" function or a solve block)
But I guess this is an exercise in programming and implementing an algorithm in Prime.
You also want the whole series of iteration steps as the result.
I spotted a couple of errors in your sheet:
1) The guess values 0;0 result in a non-invertible Jacobi-Matrix and so your function must fail
2) You defined f as a function with two arguments (x and y) but in your Newton function you used the function argument f as a function with just one vector argument. You should rewrite your input function f to accept a vector as its argument and do the very same with your function J. That way you may also be able to deal with more than two variables, using the very same function "Newton". You may just redefine J(x):=J(x[1,x[2) to save typing the definition from anew.x
At the top you are collecting the current variable values and the number of the iteration step in a matrix "result"
3) You forgot about the second matrix index (should bi "i") in result
4) When writing x_i you used the literal index instead of the vector index (Thats what the error message is trying to tell you)
Furthermore "result" in the for-loop is accidentally labelled as "function" - it must be manually re-labelled as "Variable"
5) You completely missed the correct iteration step using J(x), etc. You simply calculated the new x-value being the result of f(x).
If you correct those errors and you provide meaningful guess values, your routine should work OK (I renamed you function f to F, so I can use the previously defined function f (and g) to check the result using Primes root-function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- Prime 6.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, the root with 2 arguments is not the Newton Method
The Newton method for two equation is
Moscow Power Engineering Institute: Mathcad Calculation Server (mpei.ac.ru)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What is the main purpose?
1. Solve the set of equations.
2. (Learn how to) implement the method.
One solution of the set is easily found with Mathcad, without programming.
x is close (within a %) to 2/3, y=6*cos(1+x)-2
Succes!
Luc
symbolic solution:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's one way of doing it (I've used M15, but you should be able to use the method in Prime)::
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you are just looking for a solution, you sure would use Primes built-in methods ("root" function or a solve block)
But I guess this is an exercise in programming and implementing an algorithm in Prime.
You also want the whole series of iteration steps as the result.
I spotted a couple of errors in your sheet:
1) The guess values 0;0 result in a non-invertible Jacobi-Matrix and so your function must fail
2) You defined f as a function with two arguments (x and y) but in your Newton function you used the function argument f as a function with just one vector argument. You should rewrite your input function f to accept a vector as its argument and do the very same with your function J. That way you may also be able to deal with more than two variables, using the very same function "Newton". You may just redefine J(x):=J(x[1,x[2) to save typing the definition from anew.x
At the top you are collecting the current variable values and the number of the iteration step in a matrix "result"
3) You forgot about the second matrix index (should bi "i") in result
4) When writing x_i you used the literal index instead of the vector index (Thats what the error message is trying to tell you)
Furthermore "result" in the for-loop is accidentally labelled as "function" - it must be manually re-labelled as "Variable"
5) You completely missed the correct iteration step using J(x), etc. You simply calculated the new x-value being the result of f(x).
If you correct those errors and you provide meaningful guess values, your routine should work OK (I renamed you function f to F, so I can use the previously defined function f (and g) to check the result using Primes root-function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
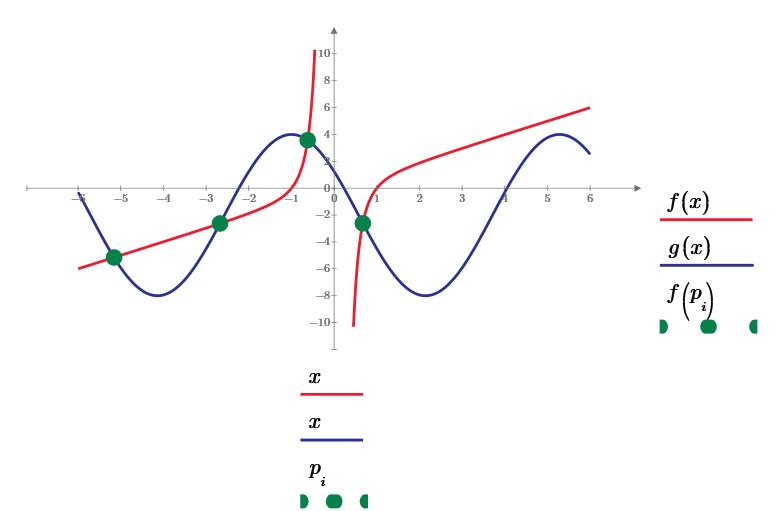
Hey, I'm just wondering if this finds the intersection points of these two functions which gives 4 different sets of values. Sorry, I'm pretty new to Mathcad so I'm still learning how to implement all these things.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@JA_9803374 wrote:
Hey, I'm just wondering if this finds the intersection points of these two functions which gives 4 different sets of values. Sorry, I'm pretty new to Mathcad so I'm still learning how to implement all these things.
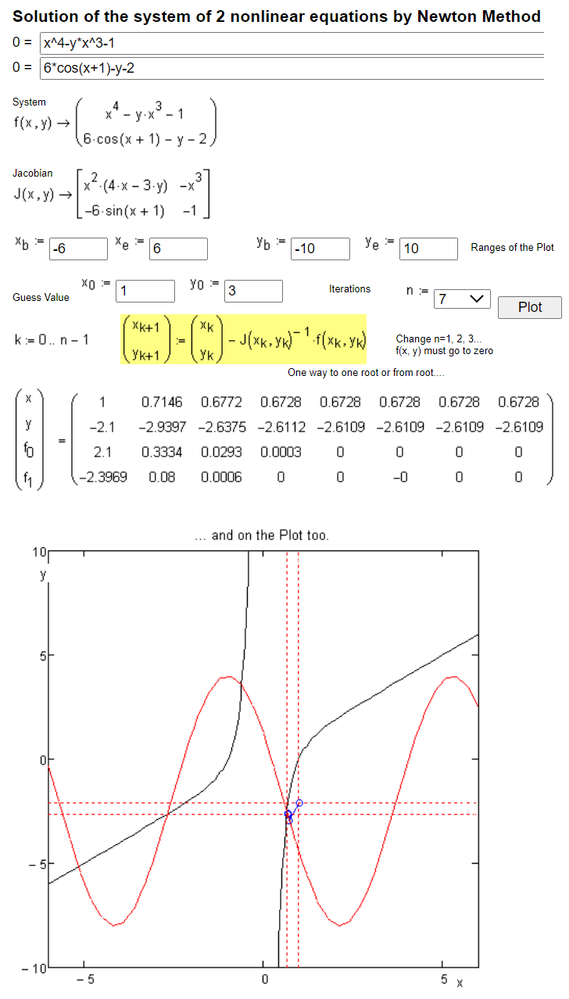
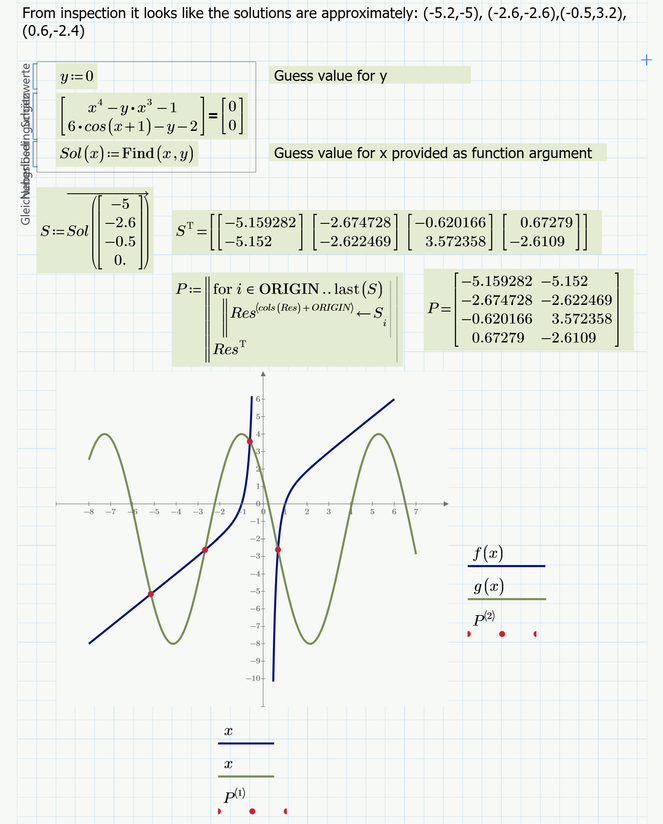
Prime is not able to find all four solutions automatically.
You have to provide either appropriate guess values or ranges, as ttokoro's picture had shown.
You can use the "root" or a solve block with "find".
In the example below I turned the solve block into a function of the guess value for x (the guess for y is constant 0).
Given the estimates you provided its possible to find all four points of intersection:
But of course you can find the same values using your own "Newton" function.
I assume you already corrected the above mentioned errors.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So I am pretty sure I fixed most of the problems and I am on a better path now. However I am struggling in how to implement the iterations needed to manipulate my variables currently. I feel like I'm close to figuring it out.
Thank you so much for the help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
However I am struggling in how to implement the iterations needed to manipulate my variables currently. I feel like I'm close to figuring it out.
I am not sure what you mean and what the problem is!?
Without seeing your sheet its hard to tell, but I guess that the iteration formula may be placed at the wrong position here
Furthermore it should rather be "x <-- ..." as as you show it you are overwriting what was collected in "result" so far. I guess the correct place to put this statement is where you had x <--- f(x) in your original sheet.
I also overlooked that your termination condition contains two errors:
1) the closing parenthesis ")" should be placed before the "<"
2) the arrow (vectorization) should contain the absolute value, too, otherwise it would have no effect.
Here is an example how to use your Newton-function to solve three non-linear equations in three variables. I compared it to Primes solve block. If you play around with the guess values you will notice, that "Newton" is more sensible with respect to the guess values and may come up with a different solution compared to Prime's solve block using the same guesses. I used Prime's "Jacob" function to create the Jacobi matrix.
P6 sheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh ok I see now, I think i was over complicating the function more than it needed to be. Thank you so much for all the help.