Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Using Solve Block to Find Zeros and Asymptotes ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using Solve Block to Find Zeros and Asymptotes ?
Hi all!
I have a problem getting the zero points and the asymptotes for my function through using Solve Block (see attachment).
For the zeros I am getting as a result from find() only one value (but the function has two zero points between 700 MHz and 2700 MHz), and this value is wrong (is not in the defined range of frequencies under "constraints").
For the values of the asymptotes no idea how to get them.
Any help please?
P.S. Is it possible to draw the asymptotes directly on the plot region?
P.S. Is there any possibility to zoom in the graph ?
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You could use the symbolic solve to get all the solutions you want - see attached. However, the disadvantage of this method is that you must get rid of the units, as the symbolic solver doesn't really understand them.
Alan
Edited to add graph with asymptotes.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You could use the symbolic solve to get all the solutions you want - see attached. However, the disadvantage of this method is that you must get rid of the units, as the symbolic solver doesn't really understand them.
Alan
Edited to add graph with asymptotes.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can also have a numerical solution, keeping the units, but you must find the roots etc individually - see attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you.
The solution is elegant with symbolic solve. As for the units, you're right. Under the ribbon "calculation" you find a button named "Calculation options". When you click on it it opens a list of item and the last one is named "units/constants in symbolics". But that didn't help much.
The solver has some real problems finding the values if the guess value is not very close to it (and it stops at the first value it finds and ignores all other solutions).
In the solution you put as a constraint Z(f) = 10^5. Is it possible to write lim (Z(f)) -> infinity?
How did you get Z(f_ix)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Doe wrote:
The solver has some real problems finding the values if the guess value is not very close to it (and it stops at the first value it finds and ignores all other solutions).
Yes, you need to look at the graph to give an idea of the useful range and starting guess.
In the solution you put as a constraint Z(f) = 10^5. Is it possible to write lim (Z(f)) -> infinity?
No. The solver doesn't like infinity. You could use a very large number like 10^300 though, if you like - not that it makes much difference to the result.
How did you get Z(f_ix)?
I defined ix as a range variable going from 0 to 2000. I then defined f using (ix+700)*10^6 to get values of f going from 700MHz to 2700MHz in steps of 1MHz. The problem with the way you defined f from k going from 700 to 2000 is that your f has 700 unnecessary zero elements (though I kept this in my version c). It works, but it's ugly!
Z(f_ix) then calculates values of Z for each value of f, running through all the values of the range variable ix.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I understood your reasoning but waht I meant with my question was how to define f_ix as a vector?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Doe wrote:
I understood your reasoning but waht I meant with my question was how to define f_ix as a vector?
If you look at my version b you will see how it is defined - half-way down on the first page.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When I write f_ix := (ix + 700)*10^6 I get an error message (concerning ix) : "This value must be a scalar or a matrix"
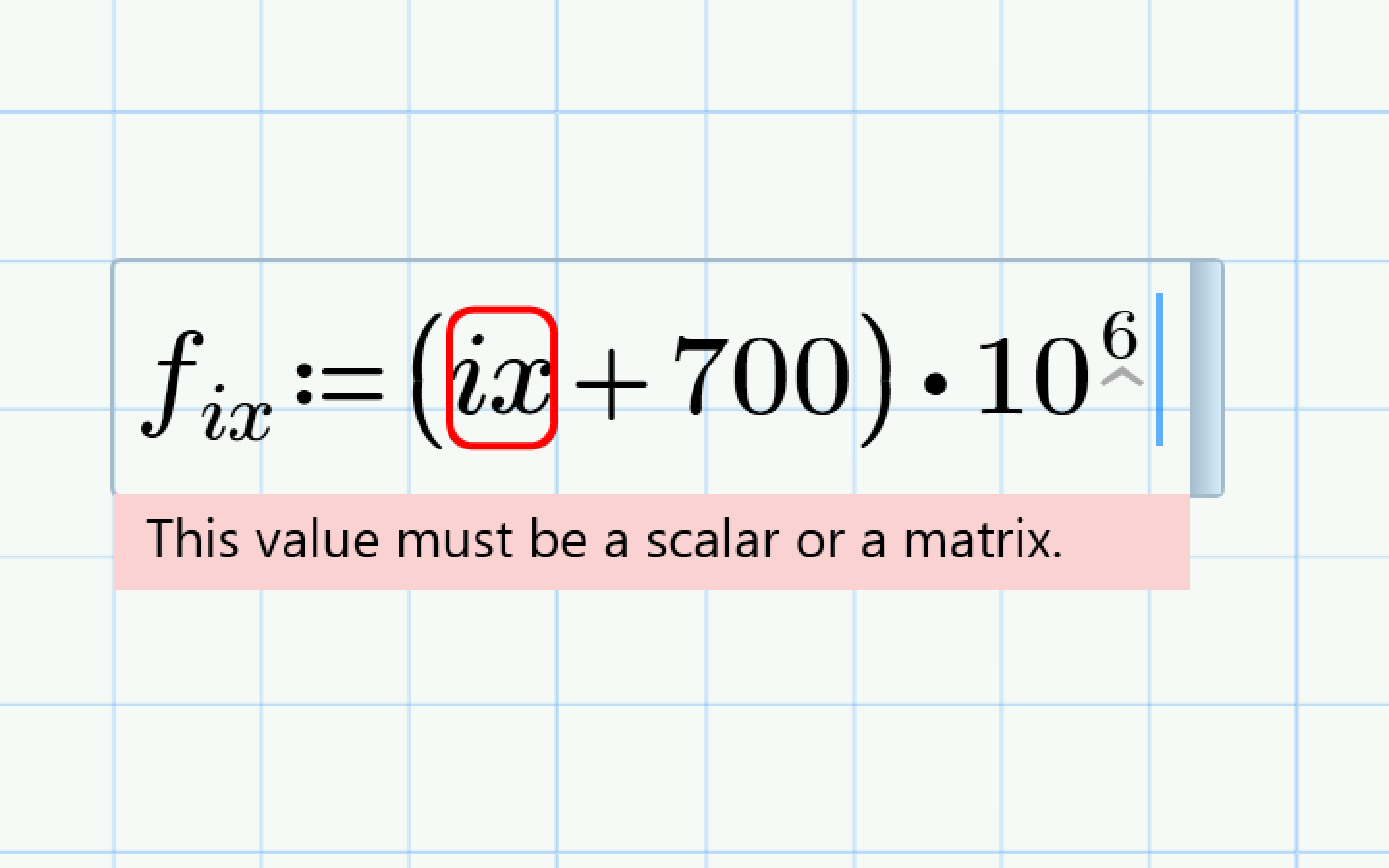
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Strange! Can you upload the worksheet where you get this?
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's actually your worksheet I tried only to reproduce the expression.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think you must have used the wrong subscript! You need to use f[ix That is, f followed by open square bracket followed by ix (or select from the Operators section of the ribbon). This will give you a true subscript. I guess you used the subscript function from ribbon. This just gives a cosmetic subscript, not something that runs through a range variable.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for the hint! It works now perfectly.





