Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
VARIABLE ALPHA EFFECT in ODEs
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
VARIABLE ALPHA EFFECT in ODEs
Hello,
Please see the attached worksheet. At the bottom of it (2- Variable alpha effect), I have explained what I am trying to obtain.
I would like to find an approximate function which defines alpha to be VARIABLE depending on x, and then substitute this NEW function into all definitions involved in solving the ODEs.
Thank you so much for your time and help,
Anousheh
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How do you change the color?
Menu Format/Equation, then choose the style you want to change (I used "User1" and changed it name to "Variables_violet"), click "modify".
To change the style of an elelemnt in a region, select it and then either use format/Equation as above or choose the style from the drop down list left to the font selector in the menu line.
These styles can be convenient, e.g. many people have created a style "complex" which is the same as "Variables" but underlined. Applying styles can be a bit cumbersome, one would wish it could be done using ricght click menu.
OK. I understand. But, why inverse?
original function f: x --> y (f(x) = y)
inverse function f^-1: y --> x
In your case:
X1: (alpha, x0) --> x
alpha: (x,x0) --> alpha
so alpha is the inverse of X1 for constant x0
Is it possible to construct a polynomial to fit the whole curve (particularly the section that quickly drops down)?
Did you play with my Version09-sheet with the degree of the polynomial fit? Number of points for x seems to have nearly no effect.
Maybe you could achieve better results with a 2-dimensional approximation for a specific constant value of x0. We have done that type of fit in recent postings of yours.
Or you may split the function in parts and doing a polyfit foreach part separetly.
I have played around with the polynomial fit and came up with versions which generate more datapoints with smaller values of x. As I suspected in an earlier post a polynomial fit doesn't seem to be appropriate for that type of function, especially it can't cope with the rapid drop at the beginning (small x values).
Find below screenshots of the four versions, all are from polynomial surfaces of fifth order and for each value of x0 there are 200 (better said 201) datatpoints for x generated. Screenshots were taken for x0=100.
Version 09 (posted earlier): datapoints for x are evenly distributed over the whole range
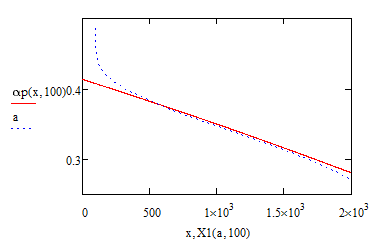
Version 10: range is split in two. 50% of all point are generated within the first 2% of the whole range. Datapoints for x are evenly distributed in each range
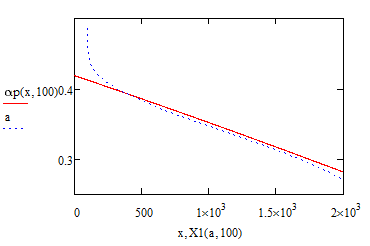
Version 11: The Datapoints for x are logarithmically distributed over the whole range in the hope to put more weight on the samller x
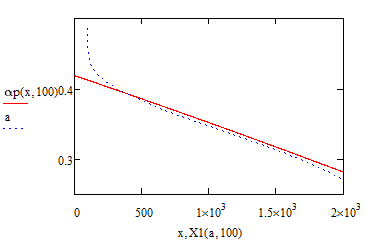
Version 12: range is split in two. 50% of all point are generated within the first 2% of the whole range. Datapoints for x are logarithmically distributed in each range
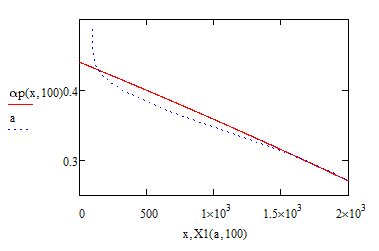
And here is a Version12 fit of order 15:

So you see that all those efforts were nearly in vain.
So you may play around with the various versions, change the order, number of points or the percentages in V10 and V12, but I doubt you will find a good fit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not entirely clear what you want, but perhaps the attached will help. There's no need to look for an approximation to alpha as a function of rho, as Mathcad can invert the relationship for you.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Alan,
Thank you so much for your reply.
I shall try to explain more clearly regarding what I really desire to obtain by posting another reply.
Thank you again,
Anousheh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its not clear to me what function you are after and how you would like to feed it back in your DEs.
I wondered why you have three almost identical DEs just for three different values of alpha, so I tried to consolidate the sheet and make the solve block parameterized to accomodate for alpha. Don't know if this would help for implementing that "variable alpha effect".
I also squeezed the sheet to four pages, one sheet wide, as I got confused with all those regions spread over to the right of the margin 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
Thank you so much for the input.
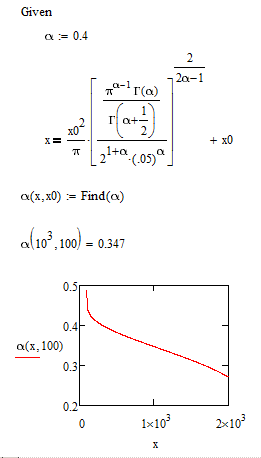
As you can see in Section 1 (which you have nicely organized it), α is a single value and I only produced some results for 3 values of α .
Please see Equation 1 highlighted in green. This is a function in which α is now a variable depending on x0. I am investigating the effect of this condition i.e. α is now a variable. The range I would like to focus is 0.3 to 0.5.
I would like to substitute this NEW function into all the appropriate equations in Section 1 and hence compare the results.
So, could you please help me find a matching function that can be substituted in Section 1 for α?
Thanks again and regards,
Anousheh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Anousheh Rouzbehani wrote:
Please see Equation 1 highlighted in green. This is a function in which α is now a variable depending on x0.
No, I don't see a depandency between alpha and x0! What I see here is a 2-dimensional function X1 which is dependent on two independent variables alpha and x0. You plotted a slice of this 2-dimensional surface for a constant value of x0 (100).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello again Werner,
Thanks.
I am sorry for this confusion. I am trying to find a polynomial that fits this curve (alpha vs. X1) and I want this polynomial to be a function of x. i.e. alpha(x,x0)=some function of x. (of course, x0=100 in our case).
Then, we should be able to fit this into equations in Section 1.
I hope you could help me now.
Anousheh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1) X1 should be x??
2) And why has it to be a polynomial? Wouldn't Alan's approach (solve block) do the job?
3) Then - in the solve block we have f(100)=1. Should it be f(x0)=1??
4) rho is now a constant (chosen from a vector). Will it be in the new approach dependent from alpha, which in turn is dependent of x=X1??
EDITED:
ad 2) see attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
x is crack size and x0 is initial crack size.
I am sure Alan's approach works. However, I prefer to have a polynomial for this study.
rho will remain constant in the new approach. It will be 10.
In Section 1, I have 3 different values for alpha. In our new approach, alpha is a function of x. for each x0. In this case, x0=100.
alph(x,x0)={some function of x} - x0 in the LHS will allow for different initial crack size to be investigated. But, we start with 100.
Thank you very much,
Anousheh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Anousheh Rouzbehani wrote:
x is crack size and x0 is initial crack size.
I don't care about the technical meaning. The important (and confusing) part seems to be that x=X1, right?
I am sure Alan's approach works. However, I prefer to have a polynomial for this study.
Haven't tried it but I fear it won't be a good ppolynomial fit.
I am sure Alan's approach works. However, I prefer to have a polynomial for this study.
Yes, see attached, while stiil some descrepancy
rho will remain constant in the new approach. It will be 10.
In your file you have rho(alpha):=g(alpha)/pi ?!
So it stays constant.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
Thank you,
This is nice. Can I transfer everything to the top of the page and substitute alpha with alpha(x,x0)?
And also, is it still possible to derive a polynomial for alpha as function of x? {alpha(x,x0)= ...}
Thank you,
Anousheh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have tried what I think you want to do, but the ODE solveblock throws an error (this value (which??) must be a scalar). Trace is not available. At the moment I have no clue what the cause is. See attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Warner,
Yes. This is what I want. Thank you.
I shall try to see what is causing the error. Should you find the problem, please let me know.
Thanks a lot.
Anousheh
PS Could you find a polynomial for alpha? Maybe this polynomial works OK!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Replace alpha() for a simple dummy function to see if the construction of alpha is the problem.
Finding a polynomial approx for alpha would be a 2-dimensional problem as of the changing x0. That makes it more difficult.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Should you find the problem, please let me know.
Which I do hereby.
The problem was that rho was (re)defined as function above.
Setting it back to a constant value makes the solve block work again. But evaluation was very slow, so I changed it a little bit by precalculating alpha - I think speed is acceptable now.
Polynomial approx still pending 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, the last one.
I tried to find a polynomial regress of third order, but its not useable, I think. Either I did something wrong or the polynomial fit really is supposed to be that bad.
See attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
Thank you so much.
1- MC=polyfitc(Xmatrix,Yvector,3) is red. I cannot see the comparison. Could you please double-check?
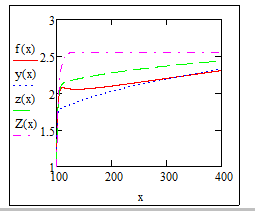
2- f(x) vs. x - This graph corresponds to the original graph of y(x), z(x) and Z(x) vs. x. This is good. In both cases, rho=10. In the original scenario y(x), z(x) and Z(x) correspond to alpha=0.4, 0.45 and 0.5 respectively.
How do I compare these graphs with f(x) - our NEW approach?
Thank you,
Anousheh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1- MC=polyfitc(Xmatrix,Yvector,3) is red. I cannot see the comparison.
I just opened the file I posted and all was OK. What is the error message? Did you change anything in the file? Could it be a version conflict? I am using Mathcad 15 M020.
For whatever its worth I attach a pdf of the file as I see it here.
I have tried a fifth order regress and it is better, but still not satisfactory for small values of x.
I attach the file "....8b" and a pdf of the vital part of it.
I guess we would get a better fit if the values for x (the inner for-loop) would not be equal spaced as they are now - we need more points at the beginning and less at the end
2- f(x) vs. x - This graph corresponds to the original graph of y(x), z(x) and Z(x) vs. x. This is good. In both cases, rho=10. In the original scenario y(x), z(x) and Z(x) correspond to alpha=0.4, 0.45 and 0.5 respectively.
How do I compare these graphs with f(x) - our NEW approach?
Just graph the functions alongside. As I have attached the new approach at the end, the other functions still are valid
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
Thanks again.
Werner Exinger wrote:
1- MC=polyfitc(Xmatrix,Yvector,3) is red. I cannot see the comparison.
I just opened the file I posted and all was OK. What is the error message? Did you change anything in the file? Could it be a version conflict? I am using Mathcad 15 M020.
I am at work now using MathCad 14. Maybe this is it! I shall open the worksheet when I am at home.
Werner Exinger wrote:
Just graph the functions alongside. As I have attached the new approach at the end, the other functions still are valid
To make sure that I am right: f(x) is a function depending on alpha(x,x0) and in our case x0=100. Correct?
Werner, what is your interpretation of above graph? i.e. how do we compare f(x) with other functions? What is the conclusion?
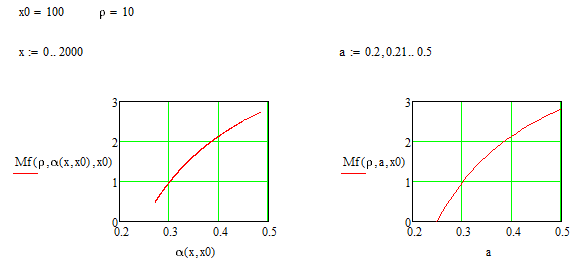
*** Would you please tell me how to plot the graph of Mf vs. variable alpha? This is another issue I have to do.
Thank you so much and regards,
Anousheh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am at work now using MathCad 14. Maybe this is it! I shall open the worksheet when I am at home.
Not sure but weren' polyfit() and polyfitc() intruduced just with version 15 as part of the new DOE features? If thats true you would have to use regress() to get the coefficients of the multivariate polynomial fit. While being cumbersome the help explains pretty well how to extract the coefficients. Is the error message about polyfitc() being unknown?
To make sure that I am right: f(x) is a function depending on alpha(x,x0) and in our case x0=100. Correct?
Yes, I simply took your definitions from the first part, excluded alpha from the parameter list (as it will not be freely choseable but be dependent an x and x0 now) and replaced variable alpha for the new function alpha(x,x0).
I guess that x0 should be a parameter of f(), too, as it is for F(), but I wasn't sure so I did not change it.
Werner, what is your interpretation of above graph? i.e. how do we compare f(x) with other functions? What is the conclusion?
I have not the faintest idea what those variables and functions are all about and how to intreprete the graphs - that's your party 😉 It looks like f(x) approaches pretty well your y(x) (constant alpha=0.4) for x>300 - whatever that may mean.
*** Would you please tell me how to plot the graph of Mf vs. variable alpha? This is another issue I have to do.
Not sure how this would make sense. The new thing is that alpha now is depending on x and x0. Your function Mf is NOT dependent on x (only on x0) So I guess x should vary for a specific x0 and you want to graph Mf over alpha. But then this graph will have nothing to do with the new function alpha - it will simply show how Mf() changes for different values of alpha ans constant values for rho and x0. Compare the two graphs below, they are identical - the left one is limited as alpha obviously has a smaller range for x in 0..2000.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
Thank you. Please see the attached worksheet. At the bottom, I cannot plot Mf.
Could you please look at it for me?
And, I could open the previous worksheet with Version 15. 🙂
Thank you again,
Anousheh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you. Please see the attached worksheet. At the bottom, I cannot plot Mf.
Could you please look at it for me?
Had a hard time finding it as of your habit to use the space to the right of the page. The reason for the error is that to the left of the plot you had defined alpha as range variable and so you have overwritten the previous definition of alpha - the function alpha is gone. Thats the reason I named the range variable a, not alpha 😉
A dirty trick, if you insist that the variable should be named alpha, is, to name it "alpha." instead of "alpha" or to assign range variable alpha a different style (Format/equation). I did the latter at the bottom of the attached sheed and changed the color for the new style to violett so you can better see the difference. But again, using the new function alpha here instead of a simple variable seems to make not much sense to me.
In a prior post you asked what can be seen in the comparison graphs. I don't know from the technical p.o.v. but you can see clearly that at the beginning (small values of x)) alpha is 0.5 but then quickly drops down, so the curves for the varioable alpha go near the curves for smaller constant values of alpha (whatever that may mean).
I just spotted that you have used in your file my old definitions of f() and F(), which call function alpha() many times more and so are much slower in execution.
BTW, in a graph above you call function alpha() a "Perfect fit". Its not a fit at all, as its no approximation. Its simply the exact (from a numeric point ov view) inverse of your function X1 (which you call "Original Equation1", so in some way it IS the original equation.
Find attached a sheet which uses regress to find a polynomial fit and makes it easy to choose the order of the polynomial and it should work in version 14, too. You can see that increasing the order (I just tried 15) makes a slighty better fit, but the problem of the bad fit for small values of x remains. Using more points for x (just tried 2000) seems to have not much effect. I still think that it can get a little better by not evenly spreading the values for x in the routine mk_matrices.
Why do you need a polynomial approximation instead of the "exact" function?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
Thank you.
Werner Exinger wrote:
A dirty trick, if you insist that the variable should be named alpha, is, to name it "alpha." instead of "alpha" or to assign range variable alpha a different style (Format/equation). I did the latter at the bottom of the attached sheet and changed the color for the new style to violet so you can better see the difference. But again, using the new function alpha here instead of a simple variable seems to make not much sense to me.
How do you change the color?
BTW, in a graph above you call function alpha() a "Perfect fit". Its not a fit at all, as its no approximation. Its simply the exact (from a numeric point ov view) inverse of your function X1 (which you call "Original Equation1".
OK. I understand. But, why inverse?
Why do you need a polynomial approximation instead of the "exact" function?
This is a part of a paper to be presented. I need a polynomial as an actual function to be shown.
Is it possible to construct a polynomial to fit the whole curve (particularly the section that quickly drops down)?
Thanks again,
Anousheh
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How do you change the color?
Menu Format/Equation, then choose the style you want to change (I used "User1" and changed it name to "Variables_violet"), click "modify".
To change the style of an elelemnt in a region, select it and then either use format/Equation as above or choose the style from the drop down list left to the font selector in the menu line.
These styles can be convenient, e.g. many people have created a style "complex" which is the same as "Variables" but underlined. Applying styles can be a bit cumbersome, one would wish it could be done using ricght click menu.
OK. I understand. But, why inverse?
original function f: x --> y (f(x) = y)
inverse function f^-1: y --> x
In your case:
X1: (alpha, x0) --> x
alpha: (x,x0) --> alpha
so alpha is the inverse of X1 for constant x0
Is it possible to construct a polynomial to fit the whole curve (particularly the section that quickly drops down)?
Did you play with my Version09-sheet with the degree of the polynomial fit? Number of points for x seems to have nearly no effect.
Maybe you could achieve better results with a 2-dimensional approximation for a specific constant value of x0. We have done that type of fit in recent postings of yours.
Or you may split the function in parts and doing a polyfit foreach part separetly.
I have played around with the polynomial fit and came up with versions which generate more datapoints with smaller values of x. As I suspected in an earlier post a polynomial fit doesn't seem to be appropriate for that type of function, especially it can't cope with the rapid drop at the beginning (small x values).
Find below screenshots of the four versions, all are from polynomial surfaces of fifth order and for each value of x0 there are 200 (better said 201) datatpoints for x generated. Screenshots were taken for x0=100.
Version 09 (posted earlier): datapoints for x are evenly distributed over the whole range

Version 10: range is split in two. 50% of all point are generated within the first 2% of the whole range. Datapoints for x are evenly distributed in each range

Version 11: The Datapoints for x are logarithmically distributed over the whole range in the hope to put more weight on the samller x

Version 12: range is split in two. 50% of all point are generated within the first 2% of the whole range. Datapoints for x are logarithmically distributed in each range

And here is a Version12 fit of order 15:

So you see that all those efforts were nearly in vain.
So you may play around with the various versions, change the order, number of points or the percentages in V10 and V12, but I doubt you will find a good fit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
Thank you so much for the time you spent on this. I really appreciate this.
I think I have received enough materials to be occupied for a while!
I shall post another request if needed.
All the best,
Anousheh






