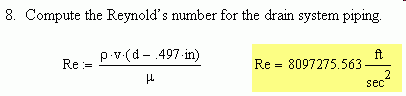- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Why is Mathcad so Keen on Units?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why is Mathcad so Keen on Units?
Find out from Mike Baldani why unit handling is such an important part of Mathcad’s product strategy.
The Mathcad blog - http://bit.ly/aOP02c
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I agree that there is a need for user defined units and dimensions (you already know I agree with you on that!), but that doesn't affect what I said. If you attach the wrong units to variables that are multiplied or divided, than you will get the wrong units in the answer. There is no way mathcad or any other CAS can trap that error, unless it somehow knows what the units are supposed to be for the answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
jean Giraud wrote:
... the other aspect of the reality is the advanced use of Mathcad
that can't support units while within Engineering works,
"must be unitless". Lot of projects had to be converted "unitless".
Maths are scalar and unitless and existed before Mathcad.
The Reynolds number is unitless. So, the Mathcad unit system fails.
The doctoring here is to apply a "reverse unit system" otherwise
some disastrous result might be expected. My orifice bore diameter metering
plate in a 12 " pipe can't be needle size neither as big as earth diameter.
My slide rules don't sing a song. This example "Reynolds number" is extracted
from Mathcad qs .
No, Mathcad's units system works perfectly because it shows that one of your example's inputs is incorrect. Had you bothered to include the parameter definitions, the error would have been immediately obvious.
TTFN
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Same comment I replied to Richard,
Not my work sheet, a Mathcad qs.
There should be a new conference,
"Mathcad Applied Unit System".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not my work sheet, a Mathcad qs.
I don't belive there is any such QuickSheet. The quicksheets with versions 13 and 15 are in XML, so I can search inside them. Only two contain the word "reynolds", and neither one shows anything even remotely resembling what you show in your gif. If there is such a Quicksheet with version 11 prove it by telling us which one it is.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Doesn't matter, a quicksheet or any other sheet with an incorrect implementation of the Reynolds number calculation is just that sheet being worng, still amply demonstrating that Mathcad's unit system is working correctly to show an erroneous calculation.
The original Civil Engineering Solved Problems E-book has a section on Reynolds number, with units, and with correct results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dan,
Kind of can of worms the units in Engineering, an endless war flames in the former Akiva. You can collect one of the work sheet used in Process Control & Instrumentation, I have more but will limit my intrusion in order not to detract other collabs preference. The best guide line is the applicable standard, having in mind the traceability, the project checkers and their nasty comments ... [Rejected, wrong calculations, not conform, not sourced ...] . I will repost this work sheet under a new thread to be recoverable for visitors.
Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi BostonDan,
"---most engineers know their units..."
This is only partially true. Knowing your units is more than a convenient agreement; it is a powerful reality check as well.
My collegues and me agree on that the raison d'etre for MathCad is the automatic unit-checking and the simplicity of reading equations. Take away the unit check and I have only 50% of my impetus left for keeping it in use.
I know there are some guys wishing that units were a thing of the past in MathCad, but they seem to be "pure" mathematicians. For the benefit of me and my kin, i.e. engineers, who'll happily keep on tainting scalars with units, MathCad without units would be only a "prettier" Excel.
Raiko
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem is more about learning what to qualify and quantify and be able to answer your own questions and be expert in your design, rather than trusting Mathcad that executes garbage-in = garbage-out. If Mathcad is your last resort, like your "supervisor", what do you do next door if your next employer does not have Mathcad and does not want Mathcad because he his fully approved and audited otherwise [like a partnership with some institution running on main frames that don't have unit systems, DOS ... etc ?]. Can you see my point besides your "Mathcad certitude & trustfulness" ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can you see my point ?
No. The fact that a task could be accomplished without a particular tool or that the tool may not be available in the future are lousy reasons to not use it when it is available and makes the task easier and the results more reliable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
jean Giraud wrote:
rather than trusting Mathcad that executes garbage-in = garbage-out.
That's just plain absurd. If you don't trust Mathcad to do that, why trust it to do ANY math? Without any units, what is your garbage detection? A sliderule? Case in point, your example, with units, is obviously in error, without knowing any further information beyond the fact that Reynolds number is dimensionless. Without units, what is your check on the validity of the garbage units?
TTFN
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>is obviously in error< [Eden]
________________________
Obviously in error, obviously not my error !
At least traceable to either of the two sources.
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
jean Giraud wrote:
Can you see my point besides your "Mathcad certitude & trustfulness" ?
Jean,
The point you are looking for is http://en.wikipedia.org/wiki/Dunning%E2%80%93Kruger_effect and the Ignobel award winning "Unskilled and Unaware of It: How Difficulties in Recognizing One's Own Incompetence Lead to Inflated Self-Assessments".
Yes, tools can lead the ignorant into danger, but that is because they are ignorant, not because of the tool. It's one of those "if P then Q" 'logic' problems.
The flip side / corolary is that whilst we teach children how to walk with scissors ("don't run with scissors"), we stop then getting near chain saws until they have learnt the first steps, and then we teach them (now adults) how to handle the chain saw. Then how to juggle one if they are in cirque du soleil.
Units and dimension analysis is a well established method of checking engineeering work. The question is how to balance the process element [simply doing arithmatic], with the two checking stages [dimensions, and units], which needs knowledge and understanding.
Philip
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dan,
I will leave this thread with the attached Mathcad QS.
It is sourced and untouched by myself except for :
1. Yellow & green
2. The note below the brown line.
Please read this note carefully. It introduces to
understanding more about designing and using
a unit system, no matter the software, though
it particularizes Mathcad in the context.
It might behave differently in versions above 11.
Don't hesitate for more questions ... etc.

Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Jean. In your attach (hcvacrat.mcd) the density rho (equal to mass by volume) is defined with units of specific weight (equal to rho times g). The formula for evaluating Reinold's number needs the density, which is an intensive propertie. Correcting the unit lbf by lb in the definition of rho gives the correct result for Re, this is, unitless, or, better say, dimension-less.
Regards. Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
Correcting the unit lbf by lb
Definately shows the need for not only proper units and their dimensions, but also a shift to the metric SI system which ahs taken the time to reduce many of these mistaken applications because it uses distinct names. SI metric still isn't perfect (can it ever be? Philosphical Q101), it needs to resolve the missing Angle dimesion, and it needs to resolve the missing "Things being counted" in Hz. Tom Gutman pointed that problem out on the collaboratory in one of the previous units round table sessions. [when it was cycles per second, one knew it was cycles being counted, now the 'cycle' part is missing!]
Philip
See attached for my Angles proposal from last year
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Very big and complex document, can take a while to understand all. So, just some few points:
1. ¿Complex angles? It's very difficult to accept by any community outside electronics eng. (maybe a few electrical's). Magnitudes are real, by "intuition".
2. Instead to add predefined dimensions I beleve that the hability to let the user to add dimensions can be more helpfull. Chemistry is an area where you must to handle a lot of quantities that lost their meaning by division, like concentrations and others. Also in the less complex world they are pressent. For example, meters of wood in a construction by surface, lets only meters. But if the wood are measured in feet, you're are in troubles. Let's the user to handle ft/m^2 as a new dimension, maybe with they own rules to simplify.
3. You analize very carefull Hz. It's amazing (for me) the way that the industry uses Hz as speed unit, like in computers. The correct unit maybe can be set as bit/sec, but not sure if is it equal to operations/sec. So, operations could be a new dimension.
4. I haven't at hand a very old book where to define forces says that because with a mass you can measure the effect of an acceleration with the a) equality -two equal mass with the same acc. have the same force and b) the proportionality -adding mass to the testing mass, then forces are well defined. This principle can apply at any other dimension.
5. You can't add apples to oranges. Or can: because both are fruits you can say: 3 fruits (apples) plus 2 fruits (oranges) equates 5 fruits. The transformation applied isn't biunivoque. This kind of troubles are common in math, just take a look for a book of complex analysis. In the transformations that you implement for complex angles I'm not sure if they are biunivoques.
For those like me, that are formed in SI system and must to work with an undiscovered american-english combination of units, mathcad's units are an excelent tool to make our lives more safe and easy.
Regards. Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>The correct unit may be can be set as bit/sec, but not sure if is it equal to operations/sec< [Alvaro]
________________________
None of those modern "Computing machinery unit" means anything. In my times of hard disk [hard = 16" dia x 3/8 " thick] the computing time unit was ms per type of operation [so much per +, -, *, / ... such & such instruction, such & such memory ...]. That reminds me story of a collab visiting the former Akiva, he declared having a bomb PC dual processor , but finally, his Mathcad was about 4 times slower than my humble Pentium IV 256 RAM !. I understand better clock-cycles and execution time. [jmG]
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alvaro,
By happy coincidence there is a BBC Radio 4 discussion on "impossible" (imaginary) numbers which aired yesterday http://www.bbc.co.uk/iplayer/episode/b00tt6b2/In_Our_Time_23_09_2010/
You will hear in the programme that one feature of these new numbers was that mathematicians had to ensure they were self consistent and didn't break existing rules, which is why I ended up having to go into so much detail for those that get rather perniketty. ! ! Tom G is actually very good at helping clarify these points.
For most folk though, being able to use simple formula accurately (with real numbers!), will help a great deal. Trigonometric functions need angles.
Finally, I'm not sure which word you meant to use at the end of point 5 "I'm not sure if they are biunivoques." Could you suggest an alternative description (or a wikipedia article 😉 ?
Philip
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Philip Oakley wrote:
Alvaro,
By happy coincidence there is a BBC Radio 4 discussion on "impossible" (imaginary) numbers which aired yesterday http://www.bbc.co.uk/iplayer/episode/b00tt6b2/In_Our_Time_23_09_2010/
Very interesting audition, but i miss a piece of paper in it, or a blackboard. First: reals. physicists don't need reals, they can leave only with rationals, and approach any physical magnitude with an interval of rationals. The lenght of the interval is the uncertainity.
Second, negative numbers. I don't agree with the discussion, I don't found difficulty expalining it. Are those numbers in the back, or at the bottom. Like celsius degrees or altitudes. More complicated is the zero number. Notice's readears saying "there are not temperature: zero degree!" are proverbial.
With complexes, here the program came more ... complex. Problem is with modern algebra books, that introduce complexes without discussions. In the oldest you can read how carefully are they treated. Firts, they are couple of sorted pairs of reals (a,b). Or, in more technical words: the elements of the cartesian product of R by R. Then old books go to define the operations with the new entities, saying always: "well, just because the complex (a,0) can be identity with the real a, let's try to conserve the most important properties of the old operations: +,-,*,/,exp,sin, etc". But always remember you that (a,0) isn't the same thing that a. (a,0) is a complex and a is a real! And remember you at a lot of times that a+b*i it's only a notation for the complex (a,b). Each definition have a full previous discussion about if it is "correct" in the sense of "usefull", but clarifiying that probably there are a lot of other correct definitions. So, introduce the operations as extensions of the similar real operations. New books looks like the formal operations are intrinsic in the new field, but they aren't.
Complexes have a very natural representation and implementation as points in the plane. Then, aren't that artificial as the history reveal. Old mathematician was impressed with the complexes properties just because they are not all translates to reals. But the plane representation must to be enough to say that they have a physical representation. So, using complexes to electromagnetics fields or other areas, must to be well accepted. For example, a book of complexes that have a very nice chapters interpreting plane fluid flows with complexes is Pollard (isn't? can't remember the author, and have not the book).
The more beatifull formula in math is, without a doubt, e^i + 1 = 0 which correlates the five more importants numbers in the history. It could be a very good starting point.
You will hear in the programme that one feature of these new numbers was that mathematicians had to ensure they were self consistent and didn't break existing rules, which is why I ended up having to go into so much detail for those that get rather perniketty. ! ! Tom G is actually very good at helping clarify these points.
Yes, I read some posts from Tom explaining what about angles and dimensions, and are very clear and are very true and real.
For most folk though, being able to use simple formula accurately (with real numbers!), will help a great deal. Trigonometric functions need angles.
Finally, I'm not sure which word you meant to use at the end of point 5 "I'm not sure if they are biunivoques." Could you suggest an alternative description (or a wikipedia article 😉 ?
http://es.wikipedia.org/wiki/Correspondencia_biun%C3%ADvoca
Sorry, can't find it in english. In the complex plane, problems about this are very ... again, complexes. You can transform apples and oranges into fruits, but can reverse the transformation: given 8 fruits, how many apples and oranges are it? When you define a complex frequencies, you do it from reals, ins't?; to ensure that you are doing the tings well, check that the correspondence is "biunívoca", mathematically equivalente to "iif" (if and only if). To have a magnitude also, a way is to prove that you can check when two are equals and adding any two. Tha'ts the case of a way to define the mass after having definitions for forces and accelerations.
Kind regards. Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Philip,
Thanks for posting your suggestions, in a such a clear and detailed way. We are reviewing them now.
Regards,
Mona
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It took me a while to figure out where that file came from, but it's an old MC8 Quicksheet (it got dropped at some point after that). It is indeed exactly as you posted it: I checked. So whoever wrote that sheet really blew it. First because they evidently didn't know what the units of density are (I knew that when I was in high school!), and secondly because they evidently also didn't know that the Reynolds number is dimensionless. If they had known that then the fact that they had made a mistake somewhere in the units would have been obvious, precisely because they used the unit system in Mathcad!
Excellent example of why engineers should use units in Mathcad. Unless the engineer is so incompetent that they don't know what the units of the result are supposed to be, anyway. But if the engineer is that incompetent then whatever they build will probably break or crash regardless of whether they use units or not!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
It took me a while to figure out where that file came from, but it's an old MC8 Quicksheet (it got dropped at some point after that). It is indeed exactly as you posted it: I checked. So whoever wrote that sheet really blew it. First because they evidently didn't know what the units of density are (I knew that when I was in high school!), and secondly because they evidently also didn't know that the Reynolds number is dimensionless. If they had known that then the fact that they had made a mistake somewhere in the units would have been obvious, precisely because they used the unit system in Mathcad!
Excellent example of why engineers should use units in Mathcad. Unless the engineer is so incompetent that they don't know what the units of the result are supposed to be, anyway. But if the engineer is that incompetent then whatever they build will probably break or crash regardless of whether they use units or not!
Thanks Richard for your collaboration in "applied units"
As you say, the source of the error is unknown [ The book ? Mathsoft ?]. Our points converge to be careful using a unit system, and that not all unit systems may be equally implemented and their coherence govern. Too many collabs prone using Mathcad unit system, in my opinion "blindly". I have extended this point by the note added in the work sheet and its importance. The ln(x), exp(x) is comfortable, but other cases wouldn't be so obvious. My point here is paramount when a result is further treated [processed] and that needs be redefined in terms of re-applying a new unit to the previous result. Taking the ln(P) [last result in the work sheet], if that ln(P) now represents °C, better make sure the suite is coherent. I'm sure you understand that I can carry my works correctly, sure also that many collabs [including Dan and PTC] do appreciate my points and recommendations. Many solvers in Mathcad must be "dimensionless" and if those solvers are needed in the suite of the project then the user must be very careful taking all precautions. It all resumes to the reality that when using units, a project is a double task : the applied maths/physics and the units. That last remark is not superfluous and was put in evidence in the "Cannonball" contest"... Simply deceptive for Philip with his unit angle fixation that is should be otherwise than mathematically defined and reworkable to suit. I hope so many viewers who read this message understand that nothing goes simple by magic.
Cheers all collabs. Jean
_______________________________
Very many users of CAS [including Mathcad] do lack the very basic maths behind the scene. Besides the memory operations and logic operations, the entire maths are only the 4 operations +, - *, / . There is no such thing as ln, exp, .... no more than the 4 arithmetic operations doing all these wonders as giving back the functions, the plots and resuming a project from simple to advanced and that the units are subjected to such restrictions to the 4 arithmetic operations as a parallel processing [per say] . Your Mathcad does more than the Mesopotamians, the Greeks, but no more basic maths !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Too many collabs prone using Mathcad unit system, in my opinion "blindly".
Using the units system blindly is no different to doing anything else blindly: it can lead to mistakes. That doesn't make using units bad though!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would also dispute the notion that "math existed before units." Almost all examples of ancient math revolved around counting objects, and measuring physical parameters. That's why integers are called "counting numbers." Pure abstract math is a modern invention.
Even the cited examples of differential equations and their corollary integral equations were created for doing physics problems. Had people not been interested in figuring rate and acceleration problems, calculus might never have neen invented. In high school, it was not unsual for our physics teacher to present calculus concepts ahead of the actual presentation of the same in calculus class.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes Eden,
In my words and for long time back in the former Akiva,, numbers and like you say "advanced numbers" starting by qualifying and quantifying. That task like you say again is the premise to applied maths/physics. That notion does not bridge well, otherwise there would be no questions about the unit systems. World is not perfect but that admission does not justify "imperfection". Interesting your findings, well explained, thanks.
Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
jean Giraud wrote:
... for Philip with his unit angle fixation ....
nothing goes simple by magic.
Cheers all collabs. Jean
Jean,
Yes, I do like to get animated by the need for Angles....
[They are where the problems are in the calculations I have to use and check. <smile> ]
regards
Philip
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just one correction to Mr. Baldani's missive. The units error problem was not directly a consequence of "NASA engineers" using the wrong units; it was a problem with their subcontractor Lockheed Martin. While most of the articles appear to me to be whitewashing the problem, the Lockheed Martin team had to have gotten a requirements document specifying SI units instead of US customary units, particularly in this day and age.
What the NASA engineers did fail at was to verify compliance of the Lockheed Martin interface requirements specification (IRS) and interface data description (IDD) to the NASA team's own IRS and IDD.
While there's been much todo about XML implementations of IRS and IDD documents, they all fail short in the area of compliance testing. In fact, it's not uncommon for so-called "one-team" implementors to have incompatible versions of the almost identical XML documents.
In my mind, it's not a units issue at all, particularly given the other missteps taken by the NASA team, to wit, failure to follow up on numerous course corrections during the flight that would have identified flight control errors arising from the units problem, as well as ignoring the final approach position error that should have at least raised a pink flag that there might be a problem.
TTFN
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I see that the original question remains "unanswered", at least, in the Dan concept. I go to try to answer it.
In words of Mike Baldani the key is " ... Mathcad’s unit handling is more than a convenience for engineers. It benefits collaboration and cross-organizational processes." That´s more true thinking in enterprises with the home in europe but agencies in america (and not only EUA, México too) or viceversa. Or it's true also with an isolated engineering using an equipament with specifications in a unit system which is not natural for him.
Why? Because " ... most engineers know their units. They know what unit system they use, what conversion factors are, and how to properly balance the units. In fact, they know this so well that they don’t have to think about it." Yes, but also because we need to use the common sense to check any result before remark it as a possible answer. To do it is a must handling the unit system in which we know the normal values. For example, I'm comfortable with results in Celsius, but have not idea about what meaning a value in Rankine scale. I must to make the conversion to be sure that the value fails into my experience of the "normal" values.
So, this is my idea about why mathcad is a very good tool for the diary engineering practice.
But, what about the other softwares? Maybe Mathcad isn't the best tool for the very old two things:
- 1) find the answer for a problem.
- showing to another this result in a way that
- the other guy understand
- the answer is self demonstrated as valid, just because I can make mistakes
- the other guy understand
Excel have a native unit converter in Analysis ToolPak. After enabling it in the addins menu, the function is CONVERT(value, unit_from, unit_to). A discussion about why is better handling units with Mathcad than with excel is, then, reduce to why is better, in general therms, with Mathcad.
Maple have also a unit package; including in version VR4. But isn't very usefull, and I don't know nobody else that use it, with the probably exception of me (acutally, I use it, but inside mathcad 11!).
Mathematica have also a unit package, but it is minimal. Actually I wrote one with some very nice features: http://library.wolfram.com/infocenter/MathSource/5511/. But the problem is when the calculations turns more complex, like integrals or differential equations, turining the unit handling in a problem more haredest that the normal unit checking. Simplification with rules inside objects that have units can turns in an obstacle run, where obstacles finally are always redundance problems.
Matlab have some few packages for handling units, but are very basics. Derive have also some definitions, but, again, can be treated as packages.
So, Mathcad isn't only a good package to complete the taskes enumerated above, is also the best, and the best by a long difference.
Regards. Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
But, what about the other softwares? Maybe Mathcad isn't the best tool for the very old two things:
- 1) find the answer for a problem.
- showing to another this result in a way that
- the other guy understand
- the answer is self demonstrated as valid, just because I can make mistakes
One of the very first things that attracted me to Mathcad was the appearance of the finished sheet; it looks like a page from a mathematics text with integrals, summations and others appearing as if I wrote the expression out by hand (except neater.) Thus, someone familiar with the engineering math (M c/I for flexural stress, for example) can follow the logic flow of my work without needing to learn a new programming language. (Okay, they may need to have range variables explained; but they already know what a vector cross product is.)
The second thing that makes Mathcad so valuable (to me) is units and unit checking. NO, I DON'T MEAN SUC!! In this thread JmG posted an example that resulted in a Reynolds Number that was not unitless. Several unit advocates pointed out that this signified an error in the sheet. (Jean was using it as an argument for not using units.) When the result of one of my calculations doesn't have the proper units it's a red flare that there's either something wrong or something I don't understand about the math.
One of my major gripes (and a source of many errors and much heartache) is that differential equation solvers don't handle units.
A mathcad sheet with the math appearing as if I wrote it and the answer appearing in the units of choice IS the best tool for having someone else understand my work (that I've found so far.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- « Previous
-
- 1
- 2
- Next »