Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
confidence function in Mathcad vs. manual calculation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
confidence function in Mathcad vs. manual calculation
Hi friends,
I really can not find the error, why the manual calculation of the std errors of the parameters are completely wrong compared with confidence function.
Can anyone help, please?
Walter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I found it: Ks and Kp was changed in the Model definition. and of course I must fit the function before. sorry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No!! I can not find the error in my sheet. Please help.

Here confidence.
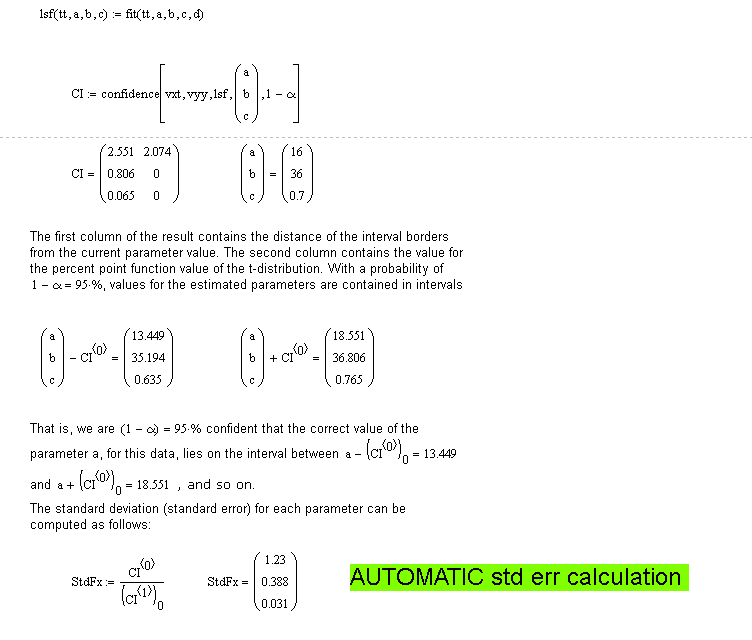
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your Covar matrix is wrong. The elements on the diagonals are variances. Since the variance is the square of the standard deviation it should never be negative.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, but the Covar calculation might be correct. Why is the Jacobian not correct? Could you take a minute to check the sheet, please?
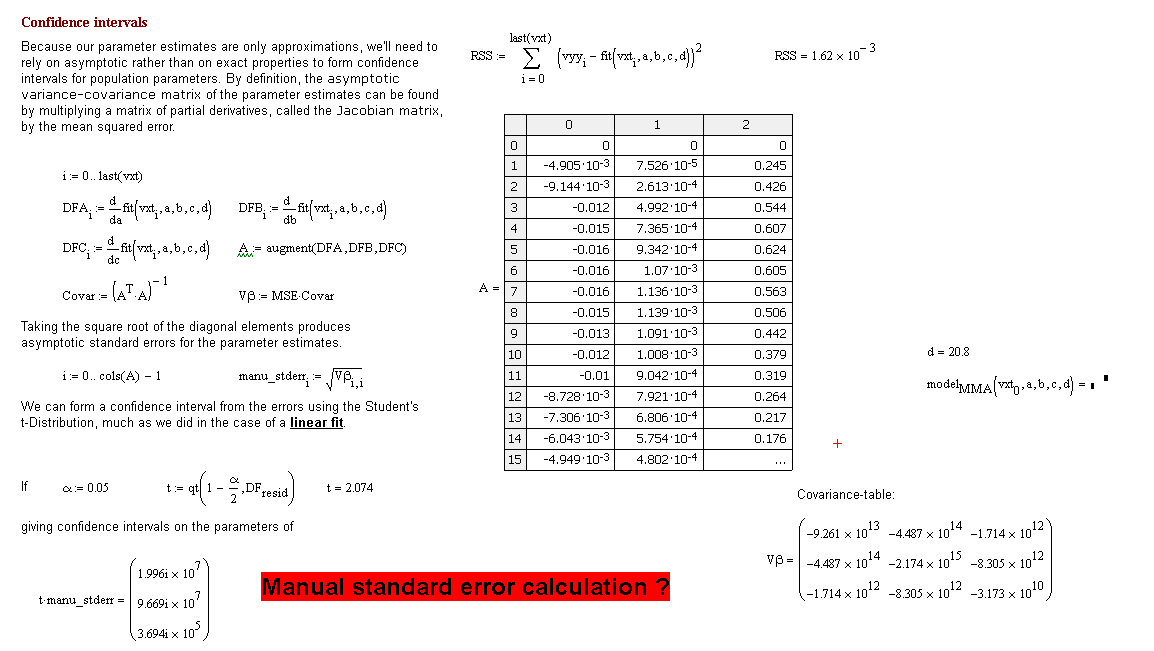
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When I do a symbolic diff (made in Mathematica and inserted as formula in the sheet on the beginning as region) the results are the same.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Right now, I can't see the problem either. The math looks correct, the implementation looks correct, and yet Covar is clearly wrong.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The strange thing is, when I put the data for curve 5 in my big sheet, it works fine. Even when I just calculate the 5th curve (below in the sheet)
I have just drag and paste the part in my short sheet.
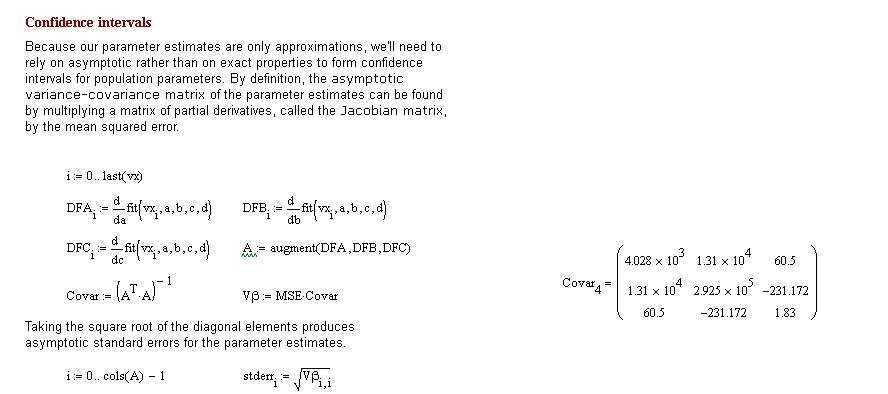

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
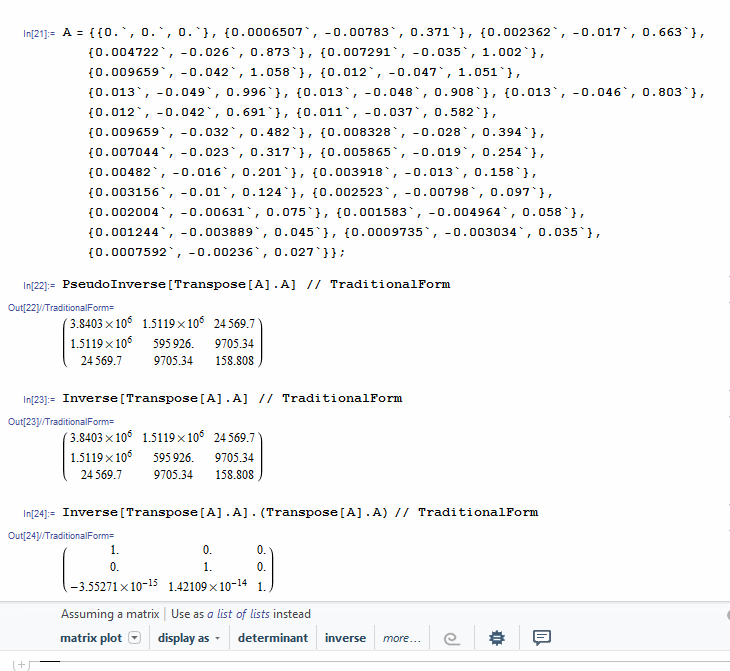
I think it's a numerical problem. I displayed A at full precision (17 digits), copied the contents to a new sheet, and the numeric engine can't invert the matrix. If you check the determinant of AT*A is very small:
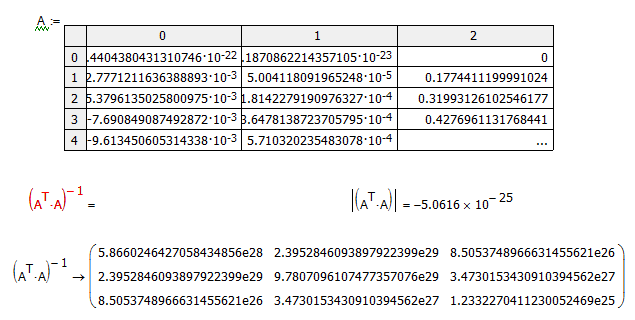
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, yes but why it works in the big sheet where I have 5 curves with different S0 but the same V, Ks, Kp. But you could be right. I will check the Matrixinversion in MMA tomorrow. Thanks a lot for your help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear friends,
I have done it also with Mathematica and got an INVERSE Error. BUT HOW can Mathematica then calculate the stderr for the Parameter with the build-in package? SO the same is with MathCAD too.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
They obviously use algorithms that are more stable for near singular matrices. Fortunately, Mathcad does offer such an algorithm with the function geninv:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks you Richard, but it depends also on the simulation data I think. Because in this model I still have great differeneces.
Maybe you could take a lot. I have there 2 cases for the model. one with 2paramter- Quadratic model and the othere the MichaelisMenten model.
The Quadratic works fine, but the MM not alsways. I would be nosey for your MC sheet where you have this cute stderr for the parameter from your picture.
Anyway thanks a lot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks you Richard, but it depends also on the simulation data I think. Because in this model I still have great differeneces.
Look at the determinant of AT*A. Now it's even smaller: about 10^-29. So just before the call to geninv put TOL:=10^-6. Then the numbers are closer, although still different. Change TOL to 10^-7. The manually calculated numbers don't change this time. That doesn't necessarily mean the manually calculated numbers are wrong though, it means that either the manually calculated numbers are wrong, or the ones from the built-in function are wrong, or both. However, since the geninv algorithm is iterative (it has to be, otherwise the results would not depend on TOL), and appears to have converged to a stable solution with TOL set to 10^-6 or less, I'm inclined to believe the manual calculation is now correct, and the built-in function is wrong because of numerical problems.
I would be nosey for your MC sheet where you have this cute stderr for the parameter from your picture.
It's just your sheet with the calculation of the inverse changed to use geninv. There are no other differences.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, Richard for your great explanation! Now I have understood.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Along similar lines: The rank of your 3x3 matrix, ATA, is only 2. If you look at the reduced row echelon form, rref(ATA), you will see that the bottom row is all zeros.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, I see. what does rref mean, and how I can interpret the result from rref? I think that the rank(ATA)= always 2 because also in this sheet, where it works, as the solution from Richards is used. Please see.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the bottom row is all zeros.
Close to all zeros, but not all zeros:
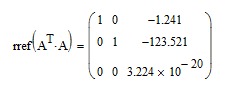
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
Close to all zeros, but not all zeros:
I admire your dedication to exactitude Richard! However, this is just numerical imprecision. In reduced row echelon form, this is going to be either a 1 or a zero. I suggest that 3.224x10^-20 is closer to zero!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's true, but the math is correct. Aside from the fact that it gives the same answer as the built-in function, I checked it against two different websites. If the matrix were truly singular it would fail, so my conclusion is that it's near singular, but not actually singular. If that is the case, then the bottom row should be 0 0 1. So rref is failing to compute the correct result. Comparing to the symbolic engine, with arbitrary precision arithmetic, confirms that:

I do not understand the symbolic result for the inverse though. I do not believe that can be correct, and it's different to the symbolic result for geninv (which is different to the numeric result).
What to believe?
Unfortunately, I just upgraded to Windows 10, and in so doing wiped out my Mathcad 11 and 13 installs, so it's not easy for me to see what the Maple engine gives as an answer. Hello LucMeekes, we need some Mathcad 11 results ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
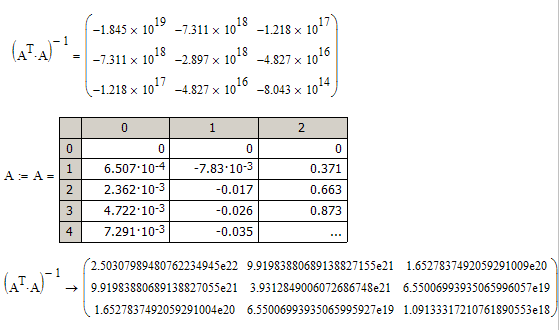
Fascinating! Also, numeric rank(ATA) = 2 and symbolic rank(ATA) -> 3
The symbolic inverse of ATA does look strange, though if you multiply it by its inverse it does a better job of getting the identity matrix than doing the same thing with the numeric geninv(ATA). On the other hand, if you use a symbolic getinv(ATA) the result, though somewhat different from the numeric result, looks reasonable and does a good job of producing the identity matrix when multiplied by its inverse! (Hmm, I've just noticed that the symbolic getinv(ATA) that I get is different from yours, though the numeric one is the same!)
I'm now getting out of my depth!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I hadn't thought about multiplying again to check the result:

So now I don't believe the numeric geninv result is correct.
Something else that is odd about the symbolic evaluation of geninv is that it does not have many significant digits. The number does not increase even if I use float,50.
It's going to be interesting to see the results from the Maple engine!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ok, Friends, its great to see that you found and looking for a solution. I will check it in MMA.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
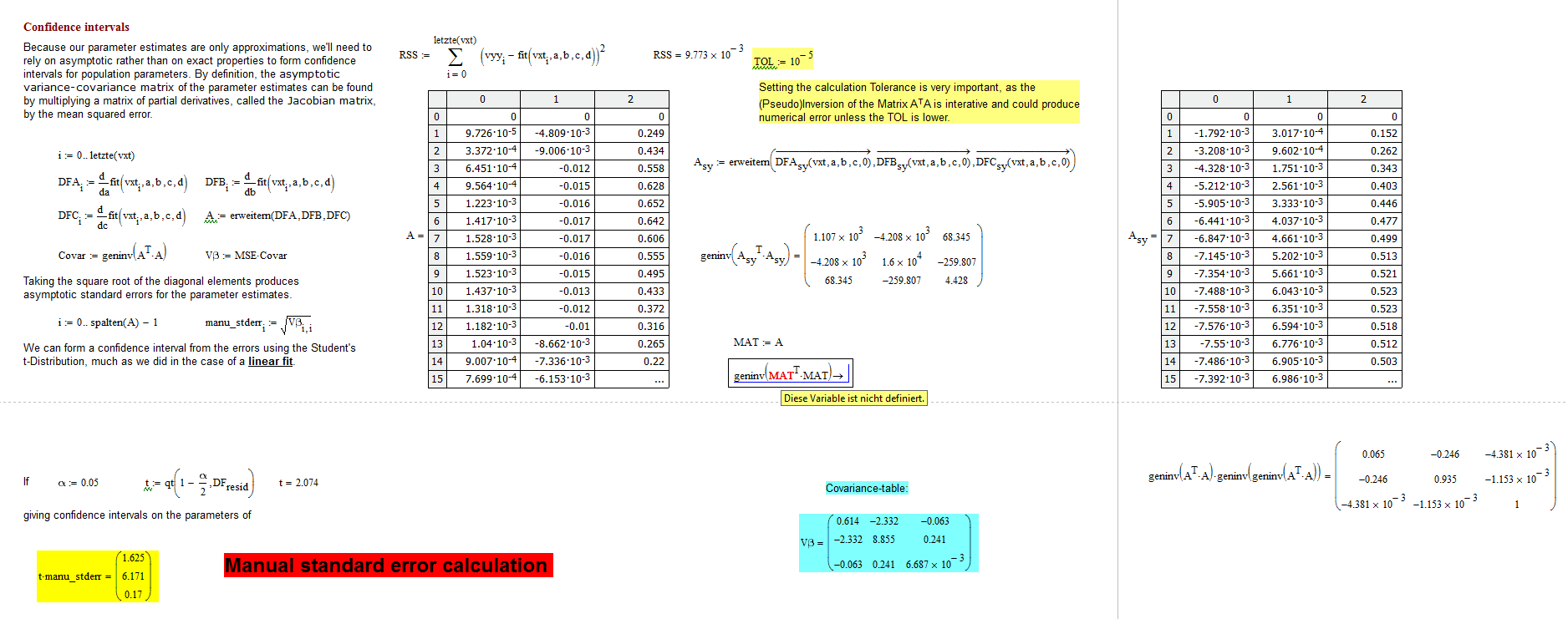
Richard, I could do your sheet here. But can you tell me why my symbolic geninv here gets an variable not defined?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have realized that you have to copy the numerical data of A in a Table, afterthat I can symb. invert. I thought that df/dx makes that nummerically. I see now, that in A there is still the symb df/dx stored. Do I think correct?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, you have to copy the data. If you don't, then the symbolic engine traces the calculations backwards through the worksheet, and when it gets to the solve block with minerr it doesn't know what to do, and fails.
Note that there is what I would consider a bug when copying data from Mathcad. It only copies the numbers at the displayed precision, not the full precision. So you need to click on the output table, then go to "format", "result", and change the number of decimal places to 17. Also, on the Tolerance tab, change the zero threshold to 307. I have never understood the reasoning behind that zero threshold, and IMO you should set it to 307 for the entire worksheet, and do so in the normal template you use when creating new worksheets. Once you have set the precision, copy the data. Given the nature of the problem, you need every digit you can get, including for Mathematica.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> I have realized that you have to copy the numerical data of A in a Table, afterthat I can symb. invert.
I guess a redefinition followed by a numeric inline evaluation should do the job as well and more convenient.
A := A =
WE
EDIT: Yes it works. The inline evaluation stops the symbolics from tracing further back and should retain the full numeric precision
(I had do diminish the table in size before adding the A:= part, I found no way doing it later)
You may also chose to use the inline eval immediately after creating the matrix

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks to verfy this. Here is the output, that MMA creates. rank 3 is correct and in MMA it comes fine.
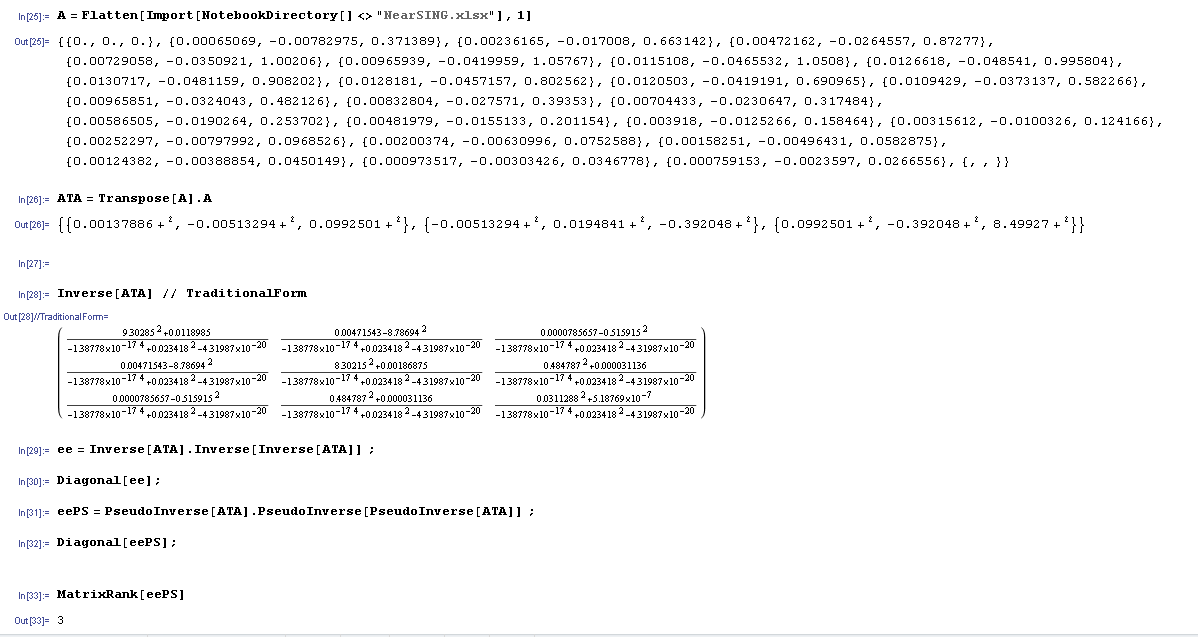
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As I mentioned in the other thread, SSE vs. ERR variable at a MinERR Solveblock?, the variables are either interdependent, or extremely close to that. At this point I am inclined to believe that it should be rank 2, and the only reason it isn't is numerical roundoff (even with the symbolic processor, because we are feeding results of numerical computations to it). I have played around with the fitting function, but algebraically I cannot eliminate one of the variables. Nevertheless, everything points to a very strong interdependence, and for data with any reasonable error you should find some other way to determine the value for one of the parameters, and then fix it during the fit. I do not know the nature of the interdependence though. Eliminating c has no effect on the quality of the fit, so c is either redundant with either a or b, or it is related to both of them in some way.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, Richard mybe you are right. Moreover I dedected Data where the Fitting Algo (LM with residuals minimizing) makes me also a little bit confused.
In anothere bigger sheet I have more different S0s, and the fitting is much more stable. Also I have checked it with MMA. I think that the more equations, with different S0 makes a big improve to the whole investigation. Here also from MMA, which has 30digits precision that is making little but significant difference.
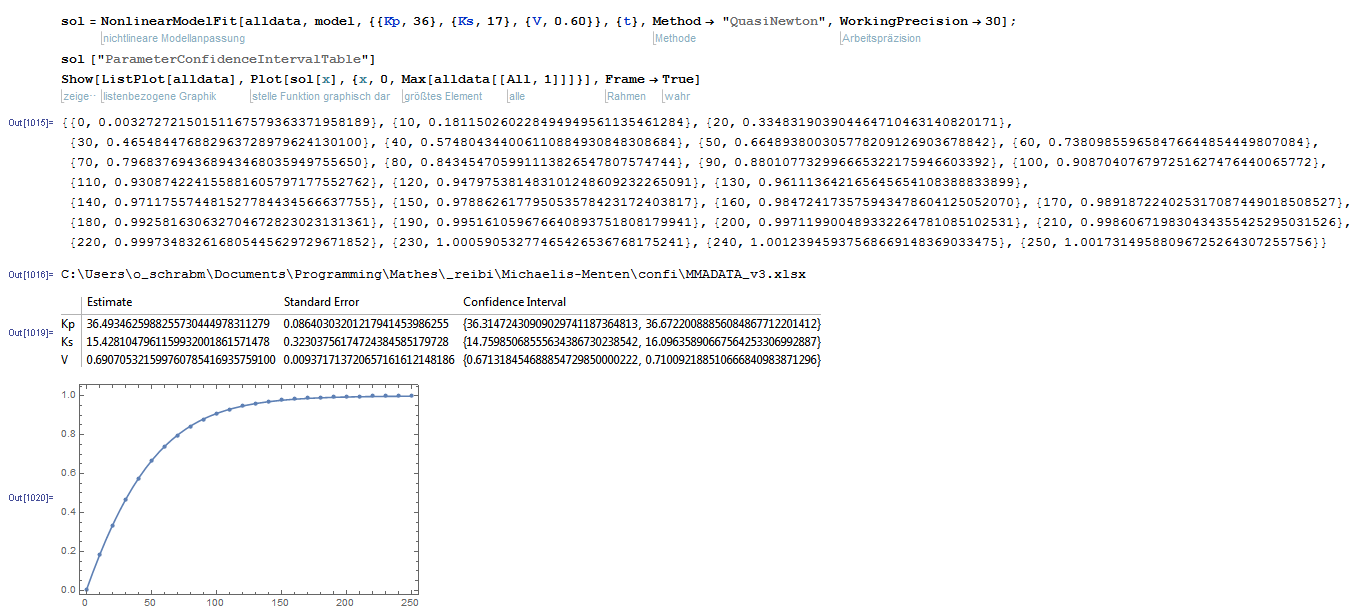
Thanks for spending your time.
Walter





