Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
coupled equation solved by odesolve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
coupled equation solved by odesolve
Dear all,
I am trying to obtain the results for two coupling equations with "odesolve". But it seems that there is some problem in it which I cannot figure out. I will be appreciated if anyone can help me with this.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"L" is undefined.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard is right in some sense.
L is defined, but as:
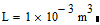
which is (most probably) not what you wanted.
So be sure to define L before the definition of
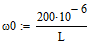 .
.
If I set L to 1 (no units, because the entire sheet appears to be unitless), I still get an error message on the Odesolve block:
"This must be an integer. The expression you used may have a fractional part."
Then if I delete Delta_r from the Odesolve, it complains:
"Found a singularity while evaluating this expression. You may be dividing by zero."
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am sorry that I forgot to delete the parameter L.
Actually there is no L and Luc is right that the problem still exist.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
These are the equations of a LASER, I believe. On that basis, I have tried to assign units to each constant and variables.
The use of odesolve, requires that the derivatives of the unknown functions must be to the first member of the equations in the solve block, furthermore all parameters must be dimensionless. After I made the change, however, it still gives me error. I would add a relationship between EI and EU, that must of course exist.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK. after deleting L there still are (at least) two errors in your sheet:
1) The last argument of odesolve is the integer number of steps, not the stepwidth, as you seem to believe. So it should not be Delta_r but rather N.
2) This is the main problem and means you will have to think about your problem again. Starting point ist r=0, but your equations contain quite a number of 1/r and 1/r^2 which means divison by zero when r=0. This sure can't work.
You can multiply both equations by r^2 to get rid of that problem and you should rewrite the equations, so the highest derivative is on the LHS.. But anyway, then the calculation does not converge to a solution then.
So maybe you would like to think about your model und your equations again, whatever they may describe.
I am not sure if scaling is also part of your problem as some of the numbers ar rather small and near the limit of numeric calculatons.
R





