Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
cspline with oscilating data
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
cspline with oscilating data
I have a curve I'm trying to fit with cspline and interp (see the attached calculation). Unfortunately, my y axis data oscilates so I had to write my function in terms of the x axis and use csort to make everything work. I was able to get a function M(phi) which works, but what I really need is phi(M) of an integral I need to perform on phi.
So, what I need to do is rewrite my function in the opposite terms (I'm not sure what the math terminology would be here). Any suggestions? What is the proper term for what I'm trying to do?
Thanks.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I checked it by choosing a value of moment ( say 375) and there are three possible curvature values that could produce this moment value.will be correct.
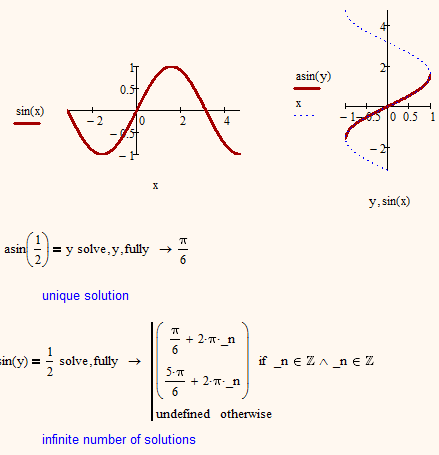
I see, so your inverse is, mathematically spoken, not a function but just a general relation which is, as you pointed ot, not unique. Functional operators like integrals are defined for functions only - the outcome has to be unique for every abscissa value, which is not true for the inverse of M(Phi). So there is not much you could do analytically with Phi(M).
What should Phi(375) yield? A vector with three values?
How would you define integration over Phi(M)?
What should be the outcome of the definite integral int(Phi(M),M,350,400)?
This wouldn't all make much sense.
The only thing you can do is to turn your inverse into a function by restricting the Phi-range like your pocket calculator does if you ask for the inverse of sinus. arcsin(0.5) yields pi/6, but of course arcsin/0.5) has an infinite number of values (pi/6 + k*2*pi and 5*pi/6 + k*2*pi, with k=integer). But your calculator (and also Mathcad) restricts the angle to the range -pi/2 to pi/2 which makes the inverse a function with unique function values and that way analytical operation like integrals are valid.
You can do the same with your Phi(M). Restrict phi to the range 0 to 0.005 (approx.) and you have a function you are able to integrate. From your graph I see you can create three different functions Phi(M). You are able to integrate each of them frim 350 to 400. But what will you do with the three results?
I am not sure if this would be of help to you. And to automatically determine the number of possible inverse functions and determinig the exact phi-ranges could be a bit cumbersome.
So whatever you have to calculate by the integral of Phi(M), either it is sufficient to use the Phi-range up to the first maximum only or there may be another way to obtain it?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was able to get a function M(phi) which works, but what I really need is phi(M) of an integral I need to perform on phi.
Its the othe way round, isn't it? In your sheet you have phi(M) and are asking for M(phi)
I can't test it without the Excel data but the attached file should help finding the inverse function(s).
I haven't looked at your various calculations before or where the data vectors come from - I just worked from the definition of your function phi_curve depending on the two vectors M_sort1 and Phi_sort1 and simply switched those vectors. Hope thats what you need.
Also showed how to get the inverse of any function using a solve block.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks,
Unfortunately, that didn't quite work, at least I don't think it did. When you sort by the moment (Y axis in the picture below) the order doesn't make sense anymore when you turn it into a continuous function. I checked it by choosing a value of moment ( say 375) and there are three possible curvature values that could produce this moment value. The cspline function when sorting by moment produces a curvature value of ~.026 which is correct in one instance, but I don't think my integration will be correct. 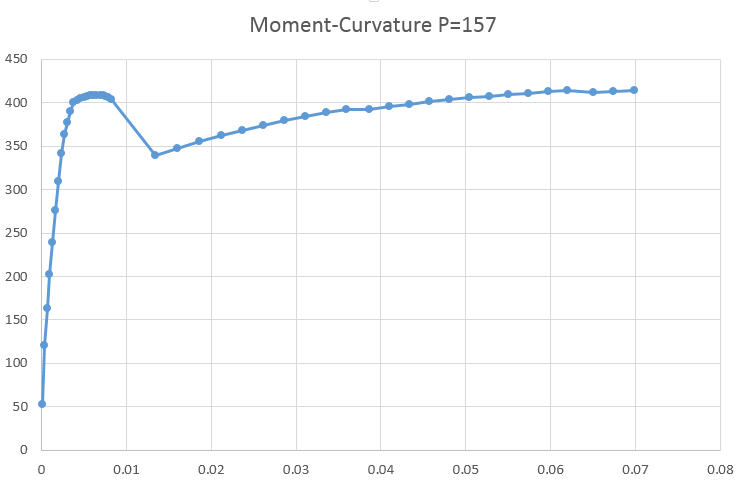
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Also, I forgot to say, but below the first portion of the calculation (original attachment) where I define the functions is an intermediate results section. I placed values from the Excel file in here so that you can see the numerical results for a particular line of Excel data.
That's where the above moment-curvature curve comes from.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I checked it by choosing a value of moment ( say 375) and there are three possible curvature values that could produce this moment value.will be correct.
I see, so your inverse is, mathematically spoken, not a function but just a general relation which is, as you pointed ot, not unique. Functional operators like integrals are defined for functions only - the outcome has to be unique for every abscissa value, which is not true for the inverse of M(Phi). So there is not much you could do analytically with Phi(M).
What should Phi(375) yield? A vector with three values?
How would you define integration over Phi(M)?
What should be the outcome of the definite integral int(Phi(M),M,350,400)?
This wouldn't all make much sense.
The only thing you can do is to turn your inverse into a function by restricting the Phi-range like your pocket calculator does if you ask for the inverse of sinus. arcsin(0.5) yields pi/6, but of course arcsin/0.5) has an infinite number of values (pi/6 + k*2*pi and 5*pi/6 + k*2*pi, with k=integer). But your calculator (and also Mathcad) restricts the angle to the range -pi/2 to pi/2 which makes the inverse a function with unique function values and that way analytical operation like integrals are valid.
You can do the same with your Phi(M). Restrict phi to the range 0 to 0.005 (approx.) and you have a function you are able to integrate. From your graph I see you can create three different functions Phi(M). You are able to integrate each of them frim 350 to 400. But what will you do with the three results?
I am not sure if this would be of help to you. And to automatically determine the number of possible inverse functions and determinig the exact phi-ranges could be a bit cumbersome.
So whatever you have to calculate by the integral of Phi(M), either it is sufficient to use the Phi-range up to the first maximum only or there may be another way to obtain it?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner. That was very clear and helpful.
I think my solution, like you said much more eloquently, is to break the data up into specific groups for which a proper function can be defined and then doing a piecewise integration based on those ranges and limits.





