- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
effect of guess values on "minimize" function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
effect of guess values on "minimize" function
Hi,
I have two different files in which I have the same function defined. For this function, I want to perform a "minimize" in order to find out its minimum across a certina interval of the variables that make up the function. I would have expected the guess values to have no effect on the rezult of the minimize, but apparently they do have (I get different results from applying "minimize" depending on the guess values I write. Does anybody know whty this happens? Below you may find a screenshot of the two different mathcad files, side by side. I have also attached the files themselves.
Thank you and best regards,
Cristian

Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a better view of the surface you try to get a minumum of. This time I plotted each "part" of it as a separate plot to avoid the artefacts inbetween.
You clearly see the asymptotic bahaviour.
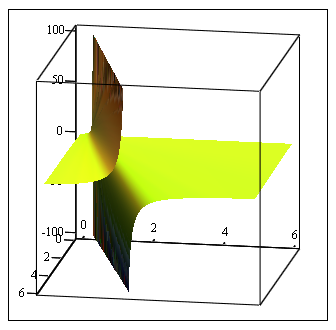
Accidentially when I just wanted to add the new 3D plot picture I deleted my previous post where I went into detail why the effect you experience is normal behaviour given the numerical algorithm and especially the specific function you try to minimize.
But by lookng at the plot you sure get the idea why it doesn't make much sense to search for a minimum of this function. You can get as close to minus infinity if you stay near the line y=1/3*(x+1). For example let x=5 and y=2.00000000001 or x=2 and y=1.000000000001.
The values you get by minize roughly follow that line, too, of course.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a better view of the surface you try to get a minumum of. This time I plotted each "part" of it as a separate plot to avoid the artefacts inbetween.
You clearly see the asymptotic bahaviour.

Accidentially when I just wanted to add the new 3D plot picture I deleted my previous post where I went into detail why the effect you experience is normal behaviour given the numerical algorithm and especially the specific function you try to minimize.
But by lookng at the plot you sure get the idea why it doesn't make much sense to search for a minimum of this function. You can get as close to minus infinity if you stay near the line y=1/3*(x+1). For example let x=5 and y=2.00000000001 or x=2 and y=1.000000000001.
The values you get by minize roughly follow that line, too, of course.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks!
Do not worry, I did manage last evening to read your initial post and that explained it all (I just did not have the time to reply then). I understand that this particular function is just an incorrectly selected example to prove the functionality of minimize and maximize so I will address that. Thank you again!
Best regards,
Cristian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fantastic explanation and effort Werner.





