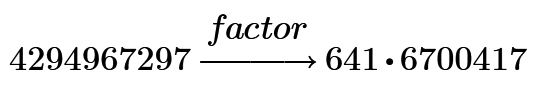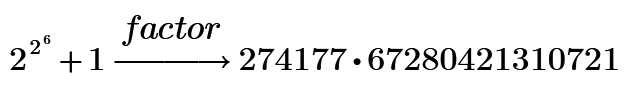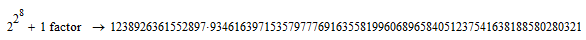We are aware of an issue causing pages to load incorrectly for some users and expect a fix soon. Sorry for the inconvenience.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
factorization
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
factorization
- Labels:
-
Puzzles Games
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And whats the motivation for doing so - hat would be the benefit?
Using a numeric solve block would limit the precision of the numbers to be used significantly and there seems to be no reason for using the symbolic "solve" as long as we have "factor".
To factor numbers in pure numeric mode you would have to write your own program - but the limitation of precision remains the same as long as you evaluate it numerically.
A numerical solution block and Prime at all are not made for dealing with number theoretic problems. An old program like Derive sure would to a better job here as it brings along a lot of useful functions for that purpose and AFAIK there also exist specialized software.
In Prime you could also play around with constraints like x=trunc(x) instead of "x in Z" or "x=integer", but I doubt that you will have success.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
How to factorize the number by using solve block?
?? Not sure what you have in mind? Maybe you can be more specific
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My Prime 6 sheet attached. Below is my question. How to use the solve block?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And whats the motivation for doing so - hat would be the benefit?
Using a numeric solve block would limit the precision of the numbers to be used significantly and there seems to be no reason for using the symbolic "solve" as long as we have "factor".
To factor numbers in pure numeric mode you would have to write your own program - but the limitation of precision remains the same as long as you evaluate it numerically.
A numerical solution block and Prime at all are not made for dealing with number theoretic problems. An old program like Derive sure would to a better job here as it brings along a lot of useful functions for that purpose and AFAIK there also exist specialized software.
In Prime you could also play around with constraints like x=trunc(x) instead of "x in Z" or "x=integer", but I doubt that you will have success.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the limit of 15 digits.
- Tags:
- Prime_6.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the list:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime 6.0 can't solve. I try to use 15, It can do soon!
However, 2^2^9+1 is hang-up!
- Tags:
- Prime_6.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
This is the limit of 15 digits.
Yes, thats the usual limit for numerical evaluation in all programs using the common IEEE data types for data storing. Thats the reason you have to use the symbolic engine for a higher degree of precision.