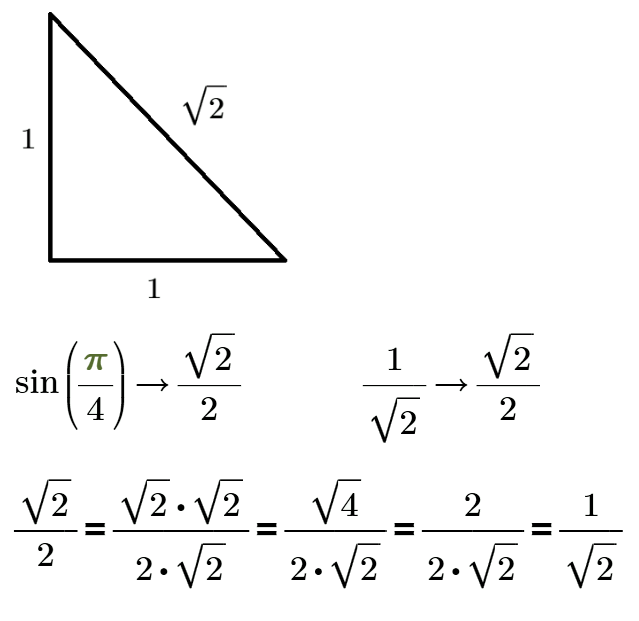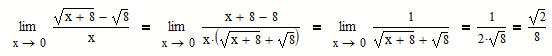Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
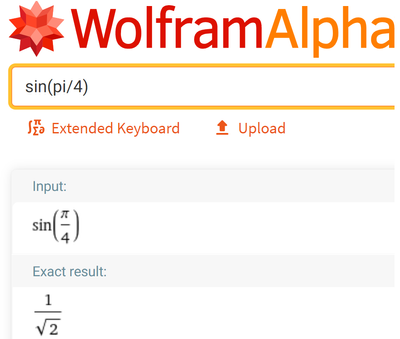
sin 45 deg
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
sin 45 deg
I had one bad mark on my math exam at school. The question was - what is the sine of 45 degrees. I immediately drew a rectangular triangle with single legs in my head and gave the answer - one divided by the root of two: the leg divided by the hypotenuse. But I heard from the teacher that the answer is wrong. The correct answer is the root of two divided by two: this is how it is written in all textbooks! And, actually, why?
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its sure NOT wrong to say that sin 45° = one divided by the square root of 2 and asking why we were drilled in school that denominators must be made rational is quite legitimate.
Its kind of a math convention and there are some reasons for doing so, though.
.) On one hand its easier to quickly estimate the value of a numerical fraction if the denominator is rational, preferably a natural number.
.) Quite often an expression is pretty simplified by rationalizing the denominator (but not always 😉
.) It may be easier to compare two fractions if the denominators are rational
.) It can make subsequent calculations easier
But of course there are situations where it would not make much sense to rationalize the denominator, for example if you are asked the value of (sin 45°)^2, it would be silly to write sin 45°= sqrt 2 / 2 as the first step, then square (2/4) and at last cancel -> 1/2.
And sometimes it makes even more sense to rationalize the nominator instead of the denominator - just think of some kind of limits like
So, is it wrong not to rationalize the denominator? No, sure not! But its kind of a convention and quite often it also makes sense to do so.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its sure NOT wrong to say that sin 45° = one divided by the square root of 2 and asking why we were drilled in school that denominators must be made rational is quite legitimate.
Its kind of a math convention and there are some reasons for doing so, though.
.) On one hand its easier to quickly estimate the value of a numerical fraction if the denominator is rational, preferably a natural number.
.) Quite often an expression is pretty simplified by rationalizing the denominator (but not always 😉
.) It may be easier to compare two fractions if the denominators are rational
.) It can make subsequent calculations easier
But of course there are situations where it would not make much sense to rationalize the denominator, for example if you are asked the value of (sin 45°)^2, it would be silly to write sin 45°= sqrt 2 / 2 as the first step, then square (2/4) and at last cancel -> 1/2.
And sometimes it makes even more sense to rationalize the nominator instead of the denominator - just think of some kind of limits like
So, is it wrong not to rationalize the denominator? No, sure not! But its kind of a convention and quite often it also makes sense to do so.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
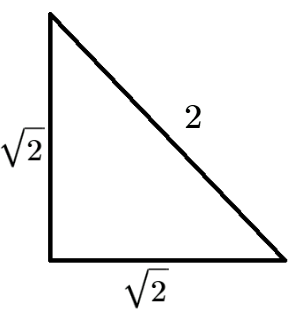
Thanks! One more triangle:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Correct answer
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Correct answer
Not sure what you'd like to say with this post?
As written above 1/sqrt 2 is as "correct" as sqrt 2 / 2 or as correct as sqrt 40/sqrt 80.
Its convention or depends on your needs, which way you write the result for further calculations and there is always much room for discussion as to which form is the most "simplified".
At school we were trained not to leave fractions with an irrational denominator, but to make the denominator rational. As already written above, this can sometimes be useful, but sometimes not.
But in any way the type of representation does not change anything in terms of "correctness"!