Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
find angles for a 3D rotation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
find angles for a 3D rotation
to all
I am trying to set up a Find() to see if I can solve the following problem
given a vector in global coordinate system (vglobal) and a vector in a local coordinate system (vlocal) so that the local co-ordinate system has rotated by angle (a,b,c)
can one find these angles? in other words if one knows the starting vector and the final (vector) can one find the transformation
problem is set up (see attached) but the exact syntax for the Find() is failing me
Thanks
Regards
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a variations which does not limit you to vectors of same length (if only the directions counts) and at least in the example given for some reason unknown to me provides the "expected" solution:

Regards
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks a lot VladimirN. Much appreciated. Will look into the proposed way of doing it
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It would make sense to turn the solve block into a function dependent on the two vectors.
Of course there are many ways to turn one point into another as long as they have the same magnitude (which is not the case with your example!), so the solve block will stop at the first one it comes by and which may not be the one you have in mind.

You can use your example, too, if you multiply vglobal by 2:
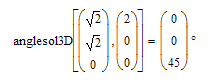
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks a lot VladimirN. Much appreciated. Didn't think about the function but for the real thing may actually be slightly "neater" approach
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a variations which does not limit you to vectors of same length (if only the directions counts) and at least in the example given for some reason unknown to me provides the "expected" solution:

Regards
Werner






