find intercept value of curve

[ptc-4915476]

Hello,

totally new to Mathcad, the help files are not of great help at all.

How do I find the Y value of the below curve where it intercepts the Y axis?

The data comes from a CSV where one column is used for X and the other for Y. My goal is to connect the start of this curve to the end. Then I would like to find the maximum difference between the straight line and the actual curve (the X value).

For now I can't even find out how to find the intersection value. I would not like to use a minimum/maximum function as the curve may look completely different for other datasets. The red line is created via the intercept function but it gives me the wrong starting value.

I appreciate the help.

[nas0k]

If you type your function "ech(posline,4000)" you should get an array or vector. It looks like the first value is where Y = 0. If you want a specific term in the array, type "ech(posline,4000)[0" to get the first value in the array.

I hope this helps.

Norm

[ptc-4915476]

Mmh, yes for this specific curve the 1st value will be ok. But I wanted to avoid using the 1st value because the 1st value might not always be the lowest.

However if I ask a more generic question. How do I find the Y value of a curve where it passes through the Y axis?

I think the "match" function can work but I can't figure out how. The "match" function seems to give me the position of the value I'm looking for (in the matrix) but not the value itself.

Let's take this example and imagine I have a CSV with two colums and the result of putting them into a XY graph gives me the following picture:

[jkowalski]

see example.

[Werner_E]

Jan, according to Prime documentation/help "regress" is outdated and becoming obsolete. Therefore that command is not documented anymore. They suggest using "polyfit" instead.

Nevertheless some tutorialfiles still utilize "regress" 🙂

[Werner_E]

you may use "lookup"

look at the attached

[Werner_E]

Have revised my sheet. Now you may use "lookup" and if thats not accurate enough you may use an interpolation (I have used cspline, but thats up to you).

[ptc-4915476]

Thank you all very much. I'll try that tomorrow and let you know if I can get it to work.

Regards

[Werner_E]

The red line is created via the intercept function but it gives me the wrong starting value.

"line" (and "intercept" and "slope") are not supposed to connect the first (or whatever) and last point of a set of data points but rather calculate the line of regression, which fits the data points best using least square fit. Its a linear approximation, not an interpolation. Usually not a single point of your data would be part of that line of regression.

What is it you want to achieve exactly? Really conncting the point of intersection with the ordinate axis with the last(?) data point? Are you sure that ther is only one ordinate value for abcissa = 0 in your vectors?

I am not sure what meaning that kind of straight line would have.

Maybe you post a worksheet with different sets of data to clarify.

[ptc-4915476]

Hello,

first of all thanks for the help.

This data represents the gain of a magnetic sensor. the X axis shows the magnetic field strength and the Y axis shows the output of the sensor in mV.

The CSV file is 400000 lines long, much to long to post it here.

The goal is to find the maximum deviation from an ideal sensor, which would be a straight line.

Therefore what I'm trying to do is to create first the ideal line connecting start and end point. I found them now with the lookup function.

But now I am stuck with the wrong slope. How do I create the slope from start to end point?

slope(startpoint,endpoint) doesn't work, it gives me an error saying something like "requires real numbers" (it's in french)

Thanks

[AndyWesterman]

If you have start & end points then fitting a line is relatively straight forward (see attached).

regards

Andy

[Werner_E]

Find attached a worksheet which does, what I think you want, but I am not sure if its really what you should do.

As I understand, you want to compare a real magnetic sensor to an ideal linear sensor. The problem in my opinion is, to define the characteristics of that "ideal sensor", apart from being linear.

Should it really be represented by the straight line through the datapoints at 0G and 4G? Both of them are for sure defective in some way as you see at 0G. Using that sensor you would have do deal with that offset of -5.3 mV anyway and an ideal sensor would have an output of 0 V there, or am I wrong?

So I think the straight line corresponding to that ideal sensor you are looking for should include the point (0G/0V) and not the sampled datapoint (0 G / -5.3 mV). As to the second point or the slope it depends upon what that sensor should do. If a specific gain at 4G (lets say 220 mV) is mandatory, then thats your second point. Otherwise you would have to define another criterion.

Nachricht geändert durch Werner Exinger Added homogenous regression to attached file

[ptc-4915476]

Almost perfect!

Because of the "near" in the lookup function the value is actually not 4G but 3.95G (I can see it in the graph). Therefore the straight line is still not meeting the endpoint. How do I find out what the real X value that "lookup" considered?

Typing

lookup(4,posField/G,posField"near")]0

works but do I HAVE TO type it again?

Thanks

[Werner_E]

lookup(4,posField/G,posField"near")]0

works but do I HAVE TO type it again?

One way which comes to my mind is typing

lookup(lookup(4, posField/G, PosOUT)[0, posOUT, posfield)[0

which is even worse.

Another solution would be using "match".

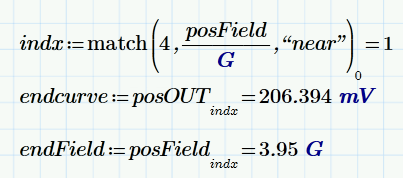
As it seems, you really want to connect first and last point of your data and ignore the whole rest of your data.

But I am still not sure how you define "first" and "last".

Obviously these are not (always) the first and last points in your datafile/datavector as you wrote earlier.

Is it always the points with field values 0 and 4 G (ar at least near) or do you want to connect the point with the lowest gain to the point with the highest gain? In that case things might be much easier to do.

Let me know.

[ptc-4915476]

The lowest gain might not be the point where the curve passes through zero of the X-axis.

The highest gain might not be the at 4G.

You are right I should maybe establish an ideal curve that is somewhere in the middle of what is indicated in the datasheet.

Nevertheless, the curve will start where it encounters 0G.

How would I find the maximum deviation of an ideal curve and the real curve.

This is just one dataset of many more I have to analyze.

I really appreciate all your help.

[Werner_E]

Steve Paul schrieb:

The lowest gain might not be the point where the curve passes through zero of the X-axis.

The highest gain might not be the at 4G.

You are right I should maybe establish an ideal curve that is somewhere in the middle of what is indicated in the datasheet.

Nevertheless, the curve will start where it encounters 0G.

How would I find the maximum deviation of an ideal curve and the real curve.

This is just one dataset of many more I have to analyze.

I really appreciate all your help.

OK, we are coming closer. The "start" of the curve is at 0G, no matter what the gain is.

The "end" of the curve is ????

a) at 4G (no, as you wrote)

b) the last point in the data set (possibly no as this would be too easy 🙂

c) at the point with the gratest gain?

d) at the point of greatest gain if its in the interval [0G; 5G] or at 5G otherwise, even if the data should go beyond?

e) I decide it myself individually for each dataset and enter it manually

f) .....??

As you have a lot of different datasets to analyze I think its important to be clear in that respect as it helps automating the whole process in Mathcad as much as possible. Best case would be to just change the name of the datafile at the top of the file, hide all calculations in a collapsed region and be presented with the max_deviation below.

Even better would be to automatically cycle through all datasets in a given directory and create a vector with filename and max_dev in it. While I think that this could possibly be made I have no idea how. This would be worth a new thread, though.

Just sent a modified file in another post. I overlooked this one of yours.

[ptc-4915476]

The initial offset is easy to compensate in electronics. (if it's steady)

Now here comes the hard part:

How do I find the maximum deviation of the real curve vs the ideal curve as indicated in the image below?

[Werner_E]

The initial offset is easy to compensate in electronics. (if it's steady)

would guess it's temperature dependent, isn't it?

What about the "first" and "last" point - or in other way spoken: what is the (your) definition for "begin" and "end" of the curve.

Concerning the horizontal deviation I think the way the line is constructed has to be reconsidered. The two curves have vertically corresponding points but usually no horizontally corresponding ones. But I'd guess thats not that difficult to deal with.

[jkowalski]

"How do I find the maximum deviation of the real curve vs the ideal curve as indicated in the image below?"

See attched file:

[Werner_E]

Are you sure that you are calculating the maximum of the horizontal deviation?

[jkowalski]

I did according to his figure. The value is about 20 mV and 1.46 G. According to me it is all right.

[Werner_E]

Sorry but I think you calculated neither the horizontal nor the vertical deviation!

The value you get is a somewhat modified vertical deviation. The correct one is simply got by max(C) in your file and is 19.042 mV. I must confess that I do not really know what "detrend" achieves and the help was not of such, at least not at first glance. But for sure "detrend" alters the data and therefore the difference.

If you add units in your sheet you will see, that the value you calculate has the unit V (a horizontal difference would have unit G or T).

For calculating the maximal horizontal deviation, or said in other words, the maximal difference of the magnetic field strength, which is 0.355 G, you need the datapoints to be aligned horizontally to make it work. Therefore I rebuilt the straight line accordingly.

Another way would be to declare a function for the ideal sensor line, but even then it had to be the inverse function to be useful - gain (in mV) in and fieldstrength (in G or T) out.

[jkowalski]

Perhaps I did not understand what was going on. My mistake.

[Werner_E]

Jan Kowalski schrieb:

Perhaps I did not understand what was going on. My mistake.

Looking at the screenshot you provided I think you mixed up abscissa and ordinate values.

[Werner_E]

Find attached my solution for calculating the desired maximum. (see page 3 and 4)

I also have included the way to connect the points with the lowest and highest gain.

[Werner_E · Accepted solution]

I have just added some comments, the maximal vertical deviation (which will not be of value, I know) and an alternate (but more cumbersome) way to define the ideal sensors characteristics via a function in contrast to the former data vector.

Just edited the file to take in account that the curve starts at 0G in any case.

Last edit for this post: added the max horizontal diff in the graph

[ptc-4915476]

Amazing!

That's what I wanted.

I'll soon be back with more annoying questions.

Thanks for your time and effort, guys!

[Werner_E]

That's what I wanted.

Fine!

 I'll soon be back with more annoying questions.

Feel free to do so 🙂

Thanks for your time and effort, guys!

You're welcome!

[ptc-4915476]

Here it comes:

How do I define a range of indexes?

Following Werners example:

posField contains data ranging from 0G to 4G. How can I limit the range in which "max" searches to a certain value contained in posField?

Ex: "max" returns a maximum deviation that lies after 3G (it considers the whole curve). I want "max" to return a maximum deviation that exists before 3G.

[Werner_E]

posField contains data ranging from 0G to 4G. How can I limit the range in which "max" searches to a certain value contained in posField?

Ex: "max" returns a maximum deviation that lies after 3G (it considers the whole curve). I want "max" to return a maximum deviation that exists before 3G.

Seems you are just answering my continous question baout the definition of the endpoint 🙂

If you want to discard all data with field greater 3G (and I assume field <0, too), I would do that at the very beginning after reading the data and proceed as shown.

I really like the new modifiers for the lookup functions. Its a pity they don't work with units.

If you need the data above 3G for some reason up to the point you calculate the horizontal diff, you would have to trim the vector hdeviation accordingly before applying max.