Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
gamma( ) function go with summation operator.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
gamma( ) function go with summation operator.
Hello, Everybody.
Thank you in advance for your time and help.
Regards.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you in advance for your time and help.
Help with what??
You are using the Gamma function as defined by Legendre (Usually Euler is credited correctly but he suggested a slighty different definition) but you seem to have no idea what this function is all about or what it looks like! So why do you use it???
I suggest you study the literature to get an idea about this meromoprh function over C and then you probably will understand why Mathcad can't evaluate that function for zero or negative integer arguments. You may even plot the Gamma function in Mathcad to get an idea. (Hints: Points of discontinuity, vertical asymptotes)
And when you are at it you may also give the definition of factorials a close look as the next error in your expression is the use of factorials of negative integers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks for your response, Werner. And :
It seems I'm missing something ?
Thanks once again.
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems I'm missing something ?
Yes - math knowledge!
Whether you are learning math or you are doing some serious work, in any case you should stick to some reliable, reputable literature rather than to blindly trust a computer software!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello, again.
Thank you in advance.
Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am confused!
You seem to know the solution, so what is the purpose of the question?
Just to see if Mathcad is capable of doing it? You saw that it is not and you have been told over and over again that Mathcad is not the right tool for that kind of calculations which you are trying to do all the time (whatever that may be anyway).
So again - Mathcad is not the right tool! It gets even worse if you partially simplify it manually and replace the inner sum by its equivalent closed expression and then tell Mathcad's symbolic to evaluate it. So if you want some fun, her you are:
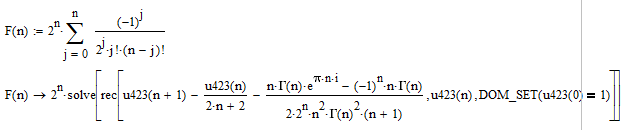
Simply replacing the expression (-1)^j by the equivalent cos(pi*j) gives you the result you expected
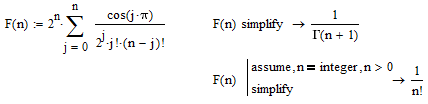
And whats the benefit? To what extent will this help you now?





