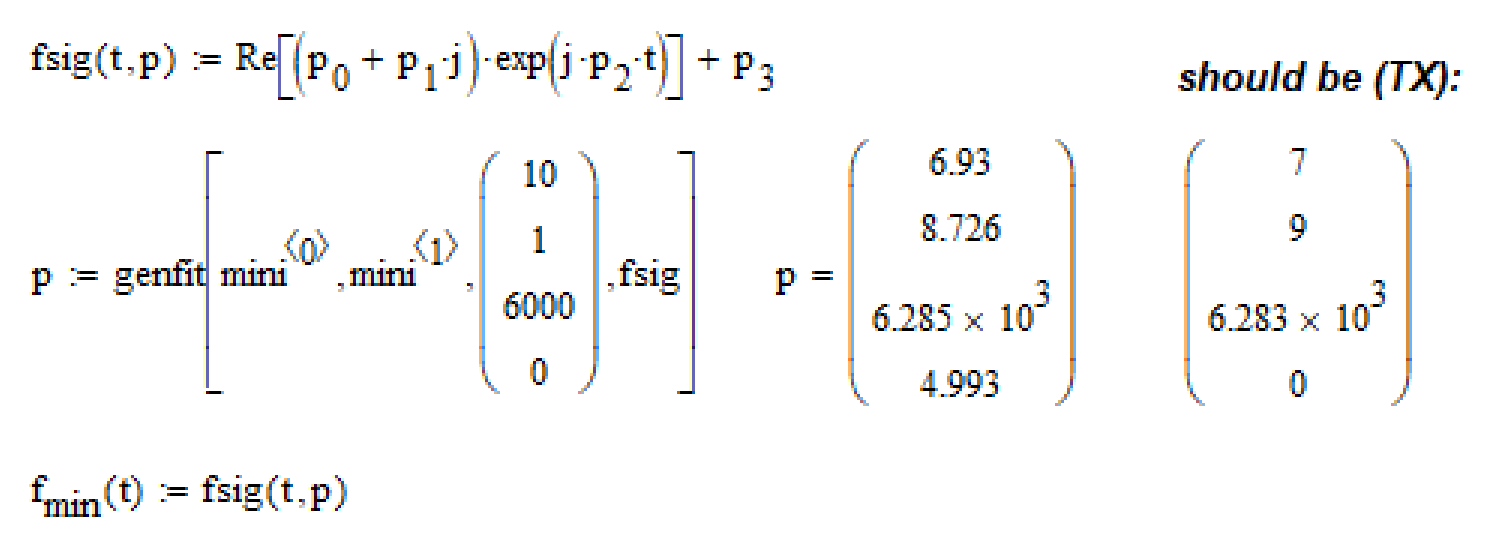Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
how to detect envelop of signal ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
how to detect envelop of signal ?
How to find upper and lower envelop of the signal ? please check my mathcad file !
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Mathcad111 wrote:
ok got it! in your file('WE_20180526_mathcad_ques-1') you have used 't' (which is basically belongs to transmitter end) but in the receiver side i don't have any idea about the time, for example if i know the exact time than i could able to find the frequency and i can used to reconstruct the 'Tx' signal, but the problem is, i don't know the exact time. could you able to do without the 'Transmitter time 't' ' (like approximation of that time).
As long as your data is sampled in equidistant time steps it should not matter what the vector t is as long as its values are equidistant and ist the same size as your data vector. But I guess it could be difficult to find working guess values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
The noise's maximum amplitude is ten times higher than that of the signal. How to distinguish a signal from such noise? it's impossible!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's not entirely impossible. A lock-in amplifier will allow to detect signals that are below the noise level. Problem is you have to know the frequency you want to detect.
The OP's problem is extremely simple as posed, but I guess he's got a more fundamental problem (doesn't know his signal and which part of it is noise).
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If the given signal is sampled, a digital notch filter tuned to the frequency of the signal should be used in such a way as to attenuate only the carrier while the noise is emitted at the output. To have the envelope a peak detector is added with a capacity ...........
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
You must break the signal into segments and find minimum and maximum of each segment.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Sorry a mistake in the lower envelope is corrected here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's extremely simple. For the problem as posed the lower enevlope is XT, the upper is XT+1.
But I guess that's not what you're after. What do you know about your signal, and what exactly are you after?
Note that Terry showed a way to estimate the envelopes, but do you need the envelopes, or are the envelopes just part of your way of what you really want to know about the signal?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Would this help?
You may play with the windows size (I have chosen 😎 and may notice some sensibility wrt the guess values of genfit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may also use your way of defining the signal for genfit.
The sensibility wrt the guesses and the window size remains though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe this old thread could be of interest, too:
https://community.ptc.com/t5/PTC-Mathcad-Questions/Phase-Shift-Problem/m-p/15134
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes it's interesting but it shows some error " D=READFILE(files, "delimited") " is not working !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You would have to download the data files from the OP as well and put them in the correct subdirectory.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ok got it! in your file('WE_20180526_mathcad_ques-1') you have used 't' (which is basically belongs to transmitter end) but in the receiver side i don't have any idea about the time, for example if i know the exact time than i could able to find the frequency and i can used to reconstruct the 'Tx' signal, but the problem is, i don't know the exact time. could you able to do without the 'Transmitter time 't' ' (like approximation of that time).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Mathcad111 wrote:
ok got it! in your file('WE_20180526_mathcad_ques-1') you have used 't' (which is basically belongs to transmitter end) but in the receiver side i don't have any idea about the time, for example if i know the exact time than i could able to find the frequency and i can used to reconstruct the 'Tx' signal, but the problem is, i don't know the exact time. could you able to do without the 'Transmitter time 't' ' (like approximation of that time).
As long as your data is sampled in equidistant time steps it should not matter what the vector t is as long as its values are equidistant and ist the same size as your data vector. But I guess it could be difficult to find working guess values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for reply,could you please explain bit more about what you doing (p1, p2) and i have posted some question regarding noise value please check my mathcad file once !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Mathcad111 wrote:
Thank you for reply,could you please explain bit more about what you doing (p1, p2) and i have posted some question regarding noise value please check my mathcad file once !
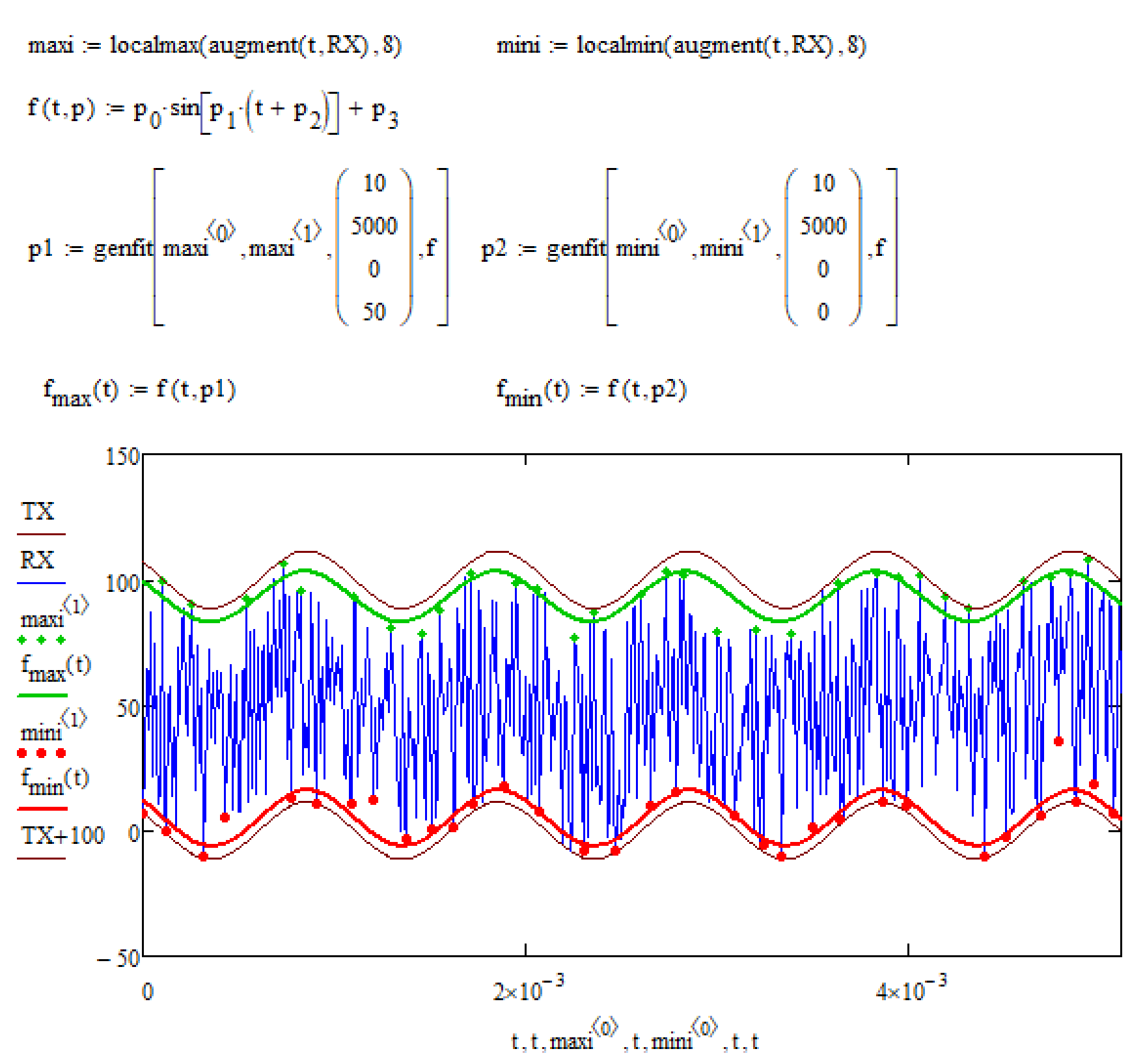
OK, lets deal with the upper envelop.
1) determine the peaks of the noisy signal using "localmax". The lower the window size (I had chosen 8 in the sheet) the less peaks were found.
2) Try to fit a function to those peaks. As the envelop obviously should be a sine, I defined a general sine function f(t,p) with four parameters (vector p). "genfit" needs guess values for the four values in p and the result is quite sensitive wrt to those guess values and I think that finding appropriate guesses automatically for various data sets is the challenge. Because I knew what the upper envelop should be (TX+100) it was easy to chose appropriate guesses 😉 In the screenshot I posted above you see the comparison between the calculated values and the expected ones.
3) define result function f.max using the parameters calculated by "genfit".
If I change in noise rnd(100) to rnd(10), the upper envelop still works, but the lower fails because local min finds not enough peaks (minima) for a decent fit. Changing the window size from 8 to 4 cures that.
But I understand that automatically chosing an optimal window size for localmax/min and optimal guess values for genfit can be quite a challange.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is not an answer to your problem. However, can the following analysis help you?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for the effort could you please upload this mathcad file (of this program) ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
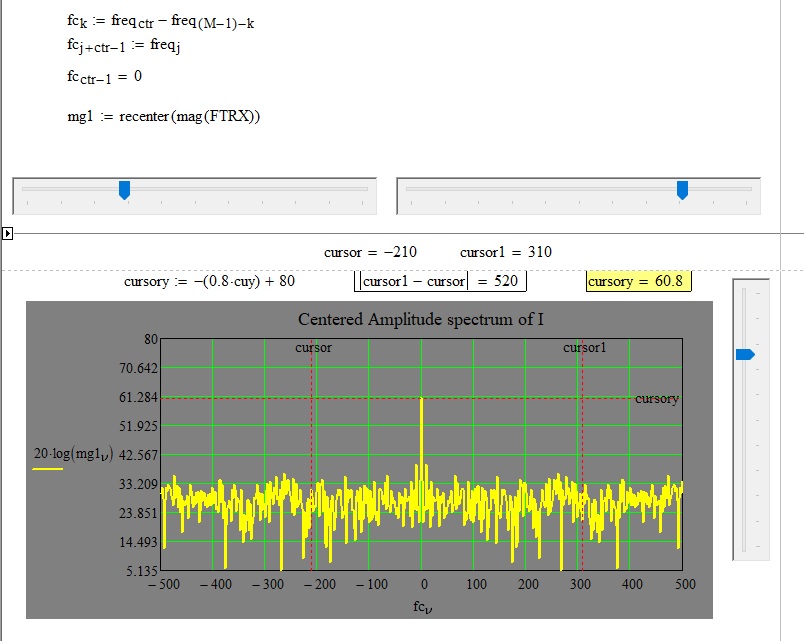
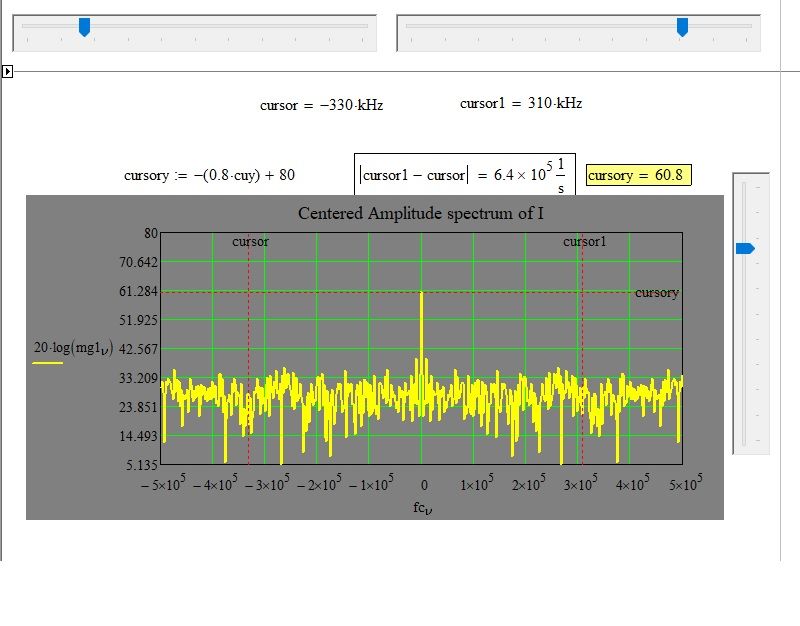
Hi,
Attached is the file with the graph with three cursors to read the values of the frequencies and the amplitude in dB
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thank for the file, but is it possible without the help of cff or fft ? and please consider this, in receiver side, i have no idea about the freq of the signal and time too what i have is only the data (like RX=[2,3,4.5,...so on])!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
cfft calculates the discrete Fourier transform of the signal placed as its argument. Obviously it does not know the frequency of the sinusoidal signal that you add up. Even the spectrum graph does not depend on f, in fact, as you can see in the following figure, I have set f = fr = 1MHz.
Since the amplitude of the noise is too high, the signal is indistinguishable, even with a PLL you will not be able to find it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes i understand that but how to calculate without CFFT ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is not clear what you want. Do you need a program that calculates the Fourier transform of a time signal equal to cfft?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Invalid solution. Wrong solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
can you upload the mathcad file ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator