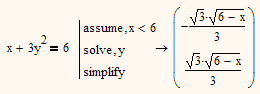Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
input x+3y^2=6
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
input x+3y^2=6
I want to input that and solve for Y. None of the equal signs seems to work. Any help?
Thanks
Joe
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Joseph Stavitsky wrote:
OK, and how do I type that equal sign please?
Also, is there some way to force real solution?
You have to use the boolean equal sign. Either from the Boolean Toolbar or via Keyboard shortcut (language dependent).
For x<=6 you get real solutions.
You can simplify each solution separate to get what you probably meant with "real solution" (it depends on x!) but it didn't work for the whole vector - we can't have it all and Mathcad's symbolics is quite limited. The result given below of course is valid for x>=6, too.
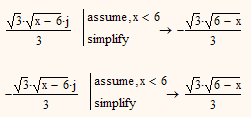
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If x is unknown you have to use the symbolic "solve" command.
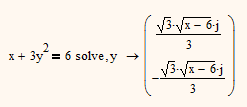
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, and how do I type that equal sign please?
Also, is there some way to force real solution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Joseph Stavitsky wrote:
OK, and how do I type that equal sign please?
Also, is there some way to force real solution?
You have to use the boolean equal sign. Either from the Boolean Toolbar or via Keyboard shortcut (language dependent).
For x<=6 you get real solutions.
You can simplify each solution separate to get what you probably meant with "real solution" (it depends on x!) but it didn't work for the whole vector - we can't have it all and Mathcad's symbolics is quite limited. The result given below of course is valid for x>=6, too.
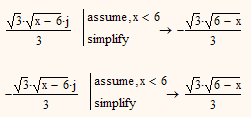
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For x<=6 you get real solutions.
The solutions are no more or less real when you do that. Sqrt(6-x) is equal to Sqrt(x-6)*Sqrt(-1). It's just that without the "assume" Mathcad chooses to write the solution in a weird way.
Interestingly, assume x is less than or equal to 6 doesn't get the simpler expression.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
For x<=6 you get real solutions.The solutions are no more or less real when you do that. Sqrt(6-x) is equal to Sqrt(x-6)*Sqrt(-1).
Yes, and what I tried to express is that neither of those two expressions is either real or not. But if you chose a specific value for x which is smaller or equal to 6, you sure get real solutions:
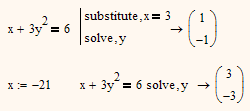
Interestingly, assume x is less than or equal to 6 doesn't get the simpler expression.
Mathcad's symbolic is famous for effects like this and especially the assume modifier very often does not work as expected and is good for producing all sorts of funny (and not so funny) effects.
I don't know why I thought that its not possible to simplify the whole vector at once - guess I made a typo and got an error. When I tried it now it worked.
While it now looks like the result would only be valid for x<6 its sure valid for all values of x
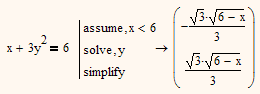
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't know why I thought that its not possible to simplify the whole vector at once - guess I made a typo and got an error. When I tried it now it worked.
While it now looks like the result would only be valid for x<6 its sure valid for all values of x
![]() . When I tried that it also didn't work! What did work was to put the assume between the solve and the simplify.
. When I tried that it also didn't work! What did work was to put the assume between the solve and the simplify.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How did you input that block-like thing? I also could not figure out how to limit the domain, so thanks for that
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Joseph Stavitsky wrote:
How did you input that block-like thing? I also could not figure out how to limit the domain, so thanks for that
I just used the keyboard short Ctrl-Shift-period and typed in the keywords, then again Ctrl-Shift-., etc., but I guess you can also just take those commands from the symolics palette one by one.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
I don't know why I thought that its not possible to simplify the whole vector at once - guess I made a typo and got an error. When I tried it now it worked.
While it now looks like the result would only be valid for x<6 its sure valid for all values of x
. When I tried that it also didn't work! What did work was to put the assume between the solve and the simplify.
Oh, thats interesting, So maybe I didn't made a typo the first time either.In the last try I simply copied regions and expressions - I didn't typed from scratch. maybe that made the trick - weird.
EDIT: Hmm, I just gave it a try and typed the expression as I had posted it from scratch - and it worked!