Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
integral calculus : a problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
integral calculus : a problem
Bonjour,
Using two type of presentations for the calculus of a classic integral , I don't have the same result.
See the joint MCD document.
Thank you for your help and Best regards
Claude
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's a matter of numerical accuracy, determined by the shape of the function in combination with the (numerical) integration method and the numerical tolerance setting. Tol=0.001 by default.
Note that the graph of the first integrand runs up steeply to high values (to positive infinity, atually) when x is near +/-1, while the graph of the second integrand is fairly smooth, and limited, hence less demanding to the type of numerical integration.
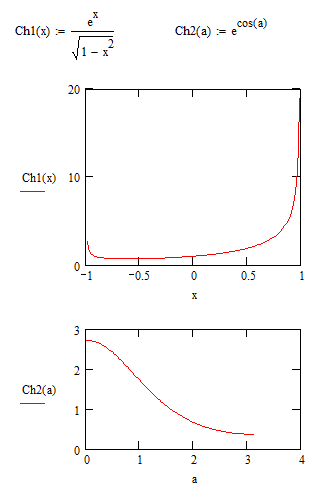
Without further specification, the numerical results are:

A noticable difference.
If you multiply each integrand with T2, you get:
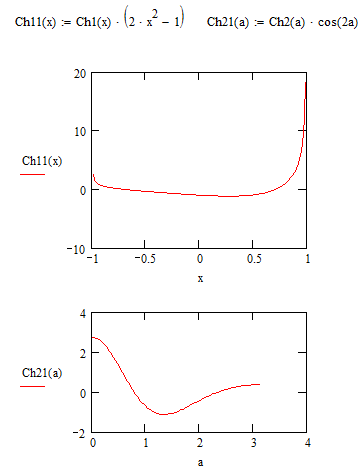
Essentially the graph for the first integrand runs less fast to infinity, and one might argue that it doesn't get there since x squared (in the numerator) dominates over x (the square root of x squared) in the denominator.
And here the integration results without further specification are:
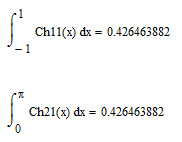
No difference in 9 decimals. Your third case gives:

No, for the first integrand, the x in the numerator would balance with the x in the denominator.
Note here that the results are also the same. In your example the error is NOT "quite the same", byt rather "quite the opposite" (minus sign!).
Anyway, with any numerical integration you should know your integrand and choose the correct method of integration and the Numerical tolerance you require.
Mathcad 11 uses by default an "adaptive" method, If I change it to Rhomberg, and set TOL=10^-9 I get:
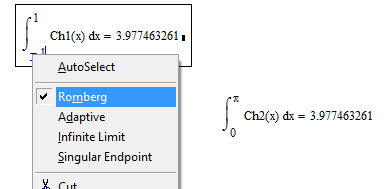
and the difference is gone.
Now, in Prime I cannot find how to control the integration methods. This may be one more of the lacking features of Prime.
The advice is: Use Mathcad (version 11 or 15). Or use the smoother function for integration...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh, by the way, if you want to know what the 'real' value of the integral is, solve it symbolically:
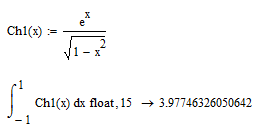
Luc





