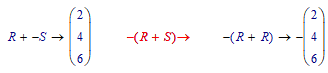mathcad 11.2a symbolic bug?

[LouP]

For those who still use it, I encountered some strange behavior in the symbolic operations of mathcad 11.2a. In my decades of using mathcad, I find it hard to believe I hadn't seen this before. Using a unary negative sign in front of a vector evaluation seems to work as expected both numerically and symbolically. However, if the unary negative vector is added to another vector of the same size, the result is a nested array.

I can't figure out what is going on. Am I just missing some expected behavior, or is this a bug?

Lou

[Werner_E]

I don't have MC11 installed and when I open your file with MC15, the strange effect is not seen, all is as expected.

Looks like in MC11 the vector with the unary minus is implicitly vectorized for some reason when evaluated symbolically.
Especially strange because usually the symbolic needs explicit vectorization in expressions where a numeric evaluation applies implicit vectorization on its own.

Maybe Luc, who still uses MC11, can shed some light on this.

[LucMeekes · Accepted solution]

Hi Lou,

Confirmed.

Negating a vector in this case behaves as though the vector is transformed into a nested vector, where each of the elements becomes a single element vector (with the negated element value.

Although...:

seems to work OK.

I think it's a bug. But it will not be fixed.

Success!
Luc

[LucMeekes]

The bug has been in there at least since Mathcad 2000:

The error is a 'no symbolic solution was found', most probably due to the fact that you cannot apply simple arithmetic to a nested matrix.

Considering that Werner doesn't see it happening in Mathcad 15, I think it is related to (the interfacing with) Maple.

Luc

[LouP]

Thanks Luc.

Good to know it's not just a mind trick on me. At least the behavior is obvious enough that it's unlikely to get by unnoticed; we are aware of it now (and knowing it's not going to change). I'll still stick by my 11.2a.

Lou