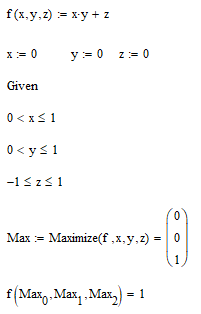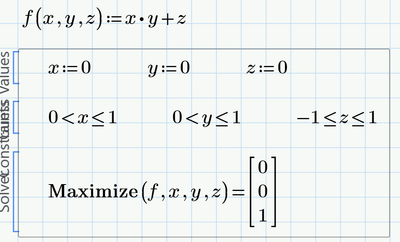maximize/minimize does not find the max/min Mathcad 15

[rnachev]

Hello,

why Mathcad does not find the maximum for this simple problem - it should be when x=1, y=1 and z=1 - in total f=2. For some reason x and y are kept to 0 even when the 0 is excluded from the range of search for x and y:

Thanks!

[Werner_E]

Maximize will treat < and <= in the constraints the same.

Maximize does not find the absolute max but only local ones! At (0;0;1) - when the algorithm slightly changes either x or y does not alter the product x*y - it remains 0. So a local max is assumed.

Changing at least one of the guess values (either x or y) slightly should give you the desired solution

[rnachev]

Thank you Werner_E!

This solves the problem, however I am not clear why Mathcad does not recognize that in fact the point x = 0, y = 0, z = 1 is in reality a minimum, not a maximum?! I guess it takes the partial derivatives with respect to x, y, z calculated at the initial guess point, sees that the partial derivatives with respect to both x and y are 0 which means we have some special point, either minimum or maximum or an inflection point, but decides that it is a maximum. Very wrong in my opinion!

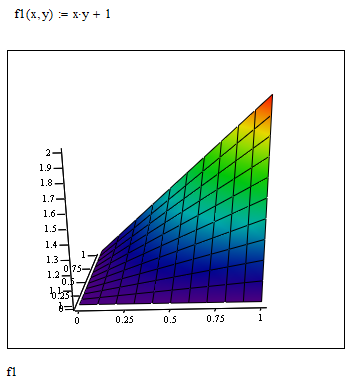
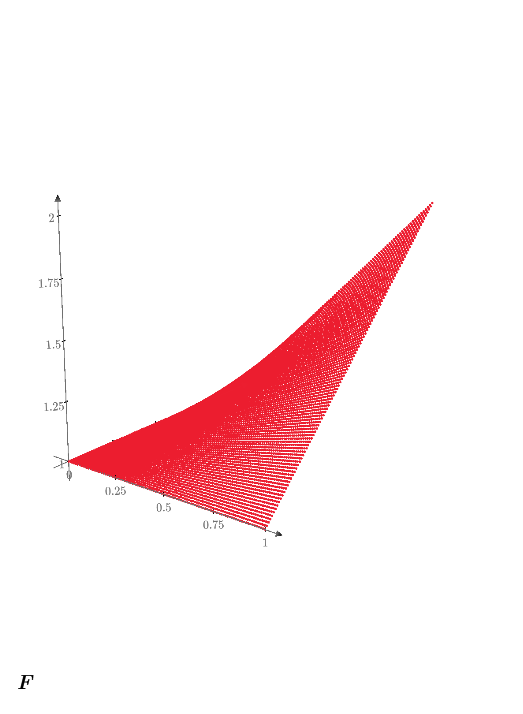
Here is the plot for z = 1:

[Werner_E]

Actually x=y=0 is neither a min nor a max if you let drop the constraints for x and y, its a saddle.

I am not sure about the conjugate gradient algorithm used by Mathcad. I may be wrong but It looks like it tries to slightly change the x value (without changing the others) and of course this does not change the result because y still is 0 and so the product x*y is zero. The same for y with x still zero. So the only change in value can be achieved by increasing z up to its allowed max of 1.

You see that Mathcad arrives at the expected solution if just one of x or y is set to a non-zero value (it may even be a negative value).

As with most numerical algorithms - sometimes the guess values are crucial.

By the way, Prime, which PTC claimed to use more modern and better numerical algorithms (a statement that has already been qualified here in the forum with some counter-examples), suffers from exactly the same problem:

So we can say that using for the guess a point where the gradient is zero may not be be the best idea 😉

[rnachev · Accepted solution]

I got the point with the small variations around the initial guess point - thanks a lot Werner_E!

Yes, you are right, I will avoid using points with zero gradient for the initial guess point! 😀

Thanks a lot! 

[ttokoro]

[Werner_E]

You will get more precision if you decrease the value of the system variable CTOL to something like 10^-6 or lower.