Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
numerical integration
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
numerical integration
I can`t to make numerical integration of function Pko(t) and Pno(t) but Pno(t) exists analytically
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think you need a better explanation of the problem.
I have tried graphing Pko(t) and Pno(t) and there seems to be something wrong with your formulae.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike, thank for answer. The formulas don`t have errors. The file z.doc contains analytical decision Pno(t).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No solution, just some observations:
Pno(t) does not throw an error but yields constantly 0 as result, which, as I guess, is not what you expected.
When I symbolically evaluate the inner integrand it surprisingly simplifies to zero. This may be due to the fact that gamma is a predefined constant. But writing gamma:=gamma should make it "unknown" at least to the symbolics - has no effect in this case. assigning gamma:=something different yields a non zero result! ?
Nevertheless, replacing gamma for some other variable name in the definition of Pno(t) does not change the result (0 for all arguments).
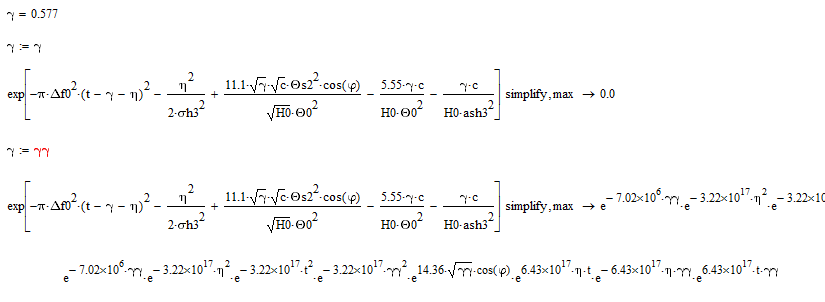
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner, thank for answer. Did you see file z.doc ? The solution which is shown in the file is not equal to zero
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
jvm jjjvb wrote:
Werner, thank for answer. Did you see file z.doc ? The solution which is shown in the file is not equal to zero
No, I didn't look at the word document. Did you typed in the result (wherever it may stem from) in Mathcad, did you plot it and could you prove its equivalent to the expression you presented in Mathcad?
Sometimes it may help to replace infinity by a bigger real number, but in your case the problem with Pno seems not to be the integrals but that the integrand simplifies to zero. Even with another variable instead of gamma, if this variable is bigger than 4*10^-6 the integrand simplifies to 0 - and you are integrating from 0 to infinity!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes, the z.doc contains symbolic integration Pno(t)





