Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
plotting a circle using points of triangle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
plotting a circle using points of triangle
Hello, i am studying master program at mechanical engineering. I am trying plot a circle using 3 points of a triangle. Circle must be plot inside triangle. How can i do? I have done my first homework but second is harder for me. I am using mathcad 15.
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Emre HAs wrote:
I am trying plot a circle using 3 points of a triangle. Circle must be plot inside triangle. How can i do?
Can you solve this problem not thru the using ready firmulas but thru using the Given-Find block ![]()
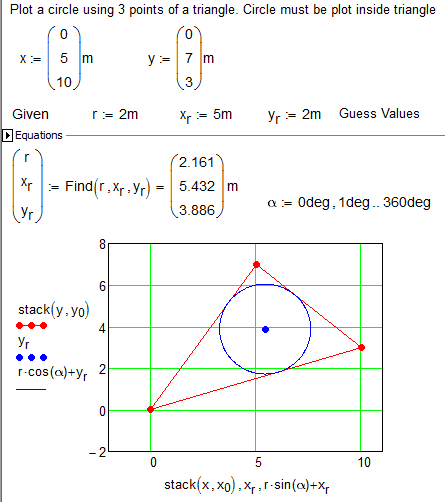
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unfortunately Emre did quite some crossposting. The inscribed circle wasn't the sole purpose and it wasn't meant to be 2D. See the "main" post here: http://communities.ptc.com/message/201417#201417
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Unfortunately Emre did quite some crossposting. The inscribed circle wasn't the sole purpose and it wasn't meant to be 2D. See the "main" post here: http://communities.ptc.com/message/201417#201417
Thanks! But the question was "Can you solve this problem not thru the using ready firmulas but thru using the Given-Find block?"
What is better (for students) - using ready (and unclear) formulas from reference books (and from Werner's solution) or searching own solution based on one formula - Pythagorean theorem:
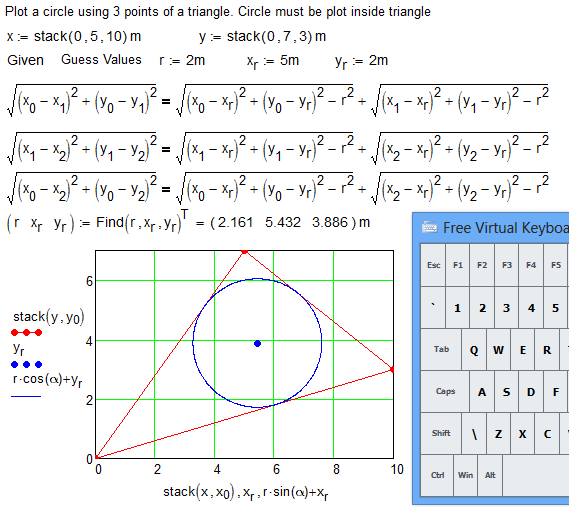
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, my fault. I thought the intent of your post was to help Emre with his problem.
My approach is: "use the resources and don't reinvent the wheel". Students have to learn to use reference books, too. Of course its our task as teachers to pose questions which can't simply be taken out of a book but require(! by the nature of the problem and not because I forbid the use refernce books) some autonomous work from their side. The task of finding the triangle inscribed circle sure is not one of those problems, while it can be quite challenging for students finding a suitable formula. If I would insist that my students deduce a formula, I would rather insist on an exact analytical one, too, and not a numeric appraoch using pushbutton Find. Nevertheless I agree that finding the equations of constraint can be a fine "finger excercise" for students.
In my reply I had chosen on purpose a formula which is not that common and was prepared being asked about it, but Emre didn't question it. Hopefully his teacher (I remember him writing "teacher is very brilliant, he sees everything") didn't asked him about ![]() .
.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is a very interesting and important educational problem.
Now students have available Reference books in Internet and available tools of symbolic and numerical solution of Math problems (Mathcad for example) - such as systems of equations.
I recommend my students to first try to resolve the problem yourself, and then use a ready-made solutions.
The best thing in teaching is to understand where it came from ready-made formula.
What solution is better:
1.
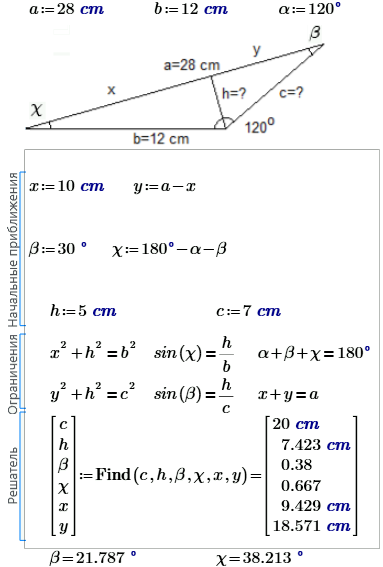
2.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I did it the long way, but I like Valery's better!
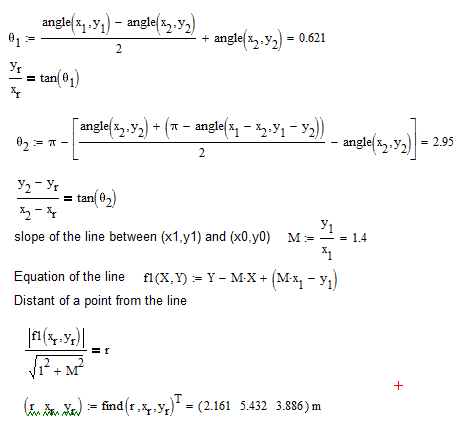
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Henry.
Do you know this problem has two solution - r and minus r.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now that I look at again, I should have just do point-to-line distant formular X3 ....
I can see there can be a minus r in your solution,
But I do not know what does a minus r mean...would you shed some light on me?
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
henry leung wrote:
But I do not know what does a minus r mean...would you shed some light on me?
Thanks
I do not know too. But second solution (-r) is solution too...
See the animation of Given-Find solution at guess values 0,0 abd 0: Video Link : 3970
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't see anything from your animation - connection rejected. Those flash apps are rather crappy. But it doen't mather. From a pure mathematical point of view -r seems to be a solution, as you equations use r exclusively in the form r^2. But as you are using the Pythagorean theorem and this theorem doesn't deal with oriented length, you have implicitely assumed by using it, that your lengths, especially r, are positive.
For whatever its worth find attached a vectorial solution using the well known distance (point-line) formula. Still a numeric approach only, but parameterized for better flexiblity.
Keep in mind, that the order of the variables is vital here to get the INscribed circle. You may try changing e.g. nv(C-B) for nv(B-C) and you will still get a circle touching all three sides but because auf the "wrong" orientation of the normal vector it will be one of the three outer circles.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, this solution does not work with units - try please A:=stack(1,1)m etc
Units help us not do errors.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For a task like this I won't need units, but of course this approach works with units, too.
Maybe you forgot to add the units to the guess values!?
Unfortunately we are not allowed to add a "SIUnitsOf(B)" here so the block would be useable with AND without units 😞

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
I don't see anything from your animation - connection rejected. Those flash apps are rather crappy.
Sorry - the animation is better here http://communities.ptc.com/videos/3971
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Werner Exinger wrote:
I don't see anything from your animation - connection rejected. Those flash apps are rather crappy.
Sorry - the animation is better here http://communities.ptc.com/videos/3971
Best animations are attached avi-files. Simple and working, downloadable, can add them to my collection if it seems worth, usable offline with any decent player, far easier to slide through frame by frame (which can be important for many Mathcad animations), etc.
Leave the video section, the like it buttons and all those things at facebook and Co. Just my 2cts.
BTW, I can't view your new animation either. Browser freezes while trying to load data from PTC. But don't bother posting it a third time, I can imagine the changes with different gues values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now I finally got it to see - how much easier would an avi have been 😉
But I am not sure what I am supposed to see here?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
But I am not sure what I am supposed to see here?
There is one type of decoration for rooms - mobile. It makes no sense, but look nice. Nerves calm down. My animations of numerican methods are one type of virtual mobile ![]() .
.
See please more interesting animation (other method for Find) in attach (for Werner) and http://communities.ptc.com/videos/3972 (for all).
I see in this animation any living creature that at first tries to break into a triangle, and then - get out of it. The creature calm down after the solution is found.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For me the best method is the transparent (KISS) method:
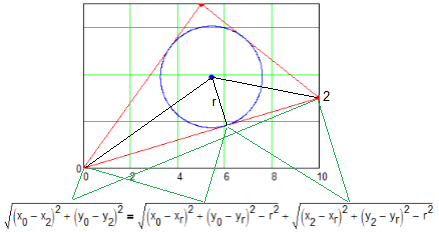
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
For me the best method is the transparent (KISS) method:
Vector analysis is transparent enough for me.
KISS? Reminds me on http://plus.maths.org/content/newton-and-kissing-problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Valery Ochkov wrote:
For me the best method is the transparent (KISS) method:
Vector analysis is transparent enough for me.
KISS?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
KISS?
![]()
We are searching a point with equal distance to three straight lines. What would be more simple than using distance formula? Not sure if that would apply for stupid, too![]()
As Einstein already said: "Make everything as simple as possible, but not simpler!" 'nough said.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
KISS?

We are searching a point with equal distance to three straight lines. What would be more simple than using distance formula? Not sure if that would apply for stupid, too
As Einstein already said: "Make everything as simple as possible, but not simpler!" 'nough said.
We are searching a point with equal distance to three straight lines... and then separately calculate the radius of the circle
We can find the point of intersection of two bisectors and then separately calculate the radius of the circle.
I think an universal meyhod to solve any geometric problem - we need to find the values of n unknowns. To do this, we must create and solve a system of n algebraic equations. Numeric with Mathcad for example. KISS!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
I think an universal meyhod to solve any geometric problem - we need to find the values of n unknowns. To do this, we must create and solve a system of n algebraic equations.
Yes, and there are so many possible ways to do so. I'd prefer a vectorial solution (or one with complex numbers) for elegance and briefness.
I tried to get a symbolic solution but was only successful in parts - unfortunately Mathcad is not very good in solving pure vector equations but maybe somebody has a good idea. See attached what I was looking for.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My way has a symbolic solution:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem is not finding a symbolic solution. My vectorial distance approach would do that, too. Please look at my file, Valery. There is a symbolic solution which is nicer and tidier and not too large to display. But its, as yours, in the six coordinates and not a sole vectorial solution in the three position vectors as I demanded. I understand that its difficult for Mathcad to recognize a vector as such unless its defined with elements.
See at the end of the file a workaround, I just was curious if someone would come up with a more direct and elegant vectorial solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just for fun here's an approach (numerical only) using polar coordinates.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Alan!
But 3 equations and 2 unknowns - sorry, may by I do not understand someone.
And second.![]()
Now I am helping to translate into Mathcad one book of problems in electrical engineering.
I see in this book imaginary currents, imaginary voltage, imaginary resistance, imaginary power, etc.
I ask authors: "Guys, do you know that in nature there is no imaginary currents, voltage, resistance, power, etc."
The authors answer me that they know about it. Then I ask them, "Why did you mislead students and tell them about the imaginary currents, voltage, resistance, power, etc.?" The authors answer that they do it to use mathematics of complex numbers. Then I ask them, "Did you know that there is a modern computer tools to solve these problems without using of electrical imaginary values." The authors reply that... "You can not teach an old dog to new tricks" and "An old horse (ox) not spoil the furrow." (what is the English equivalents of this Russian proverbs?) ![]()
![]()
I use at home two type of electrical power - real and imaginary. I pay for real power real money and for imaginary one - imaginary money ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Thanks, Alan!
But 3 equations and 2 unknowns - sorry, may by I do not understand someone.
X has two components: one real, oine imaginary, so in total there are three unknowns.
. "You can not teach an old dog to new tricks" and "An old horse (ox) not spoil the furrow." (what is the English equivalents of this Russian proverbs?)
The "old dog, new tricks" is well known in English, but I'm not aware of another similar to the "old horse (ox).." one. ![]()
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not a vectorial solution but offer an alternative
the equation is from wikipedia under proof 1 of http://en.wikipedia.org/wiki/Distance_from_a_point_to_a_line
I have to square the formula and the R is really radius square because symbolic solve cannot solve with the | |
but the squared formula coz me run out of memory. so I cannot even save with the squared formula..
please square the left hand side in the symbolic solve and see if you can finish the calculation
I hope I put in everything correctly for the formula....
by the way, the calculation assume one of the vertex of triangle is at the origin...even if this worksheet works, a general solution is still needed with simple transformation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can anyone help me to make this file work?
I find the distant using cross product but the solve block cannot find a solution





