Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
quadratic equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
quadratic equation
I am trying to put my calculations for concrete footings into MathCAD and can't get this to cooperate. With numbers, it looks like this . . .
The answer is approximately 13.08, but I can't seem to figure out how to set it up in MathCAD 14 to automate the calculation. Any insight/help would be appreciated. I tried to work through the help section, but I can't get this one to cooperate.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Send pleace the Mathcad-file!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery,
I don't have a file for this, just trying to work through some of the calculations and get them in MathCAD so I don't have to manually input them.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Use the Boolean equals.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are many ways to do this in Mathcad. Alan shows one, using the symbolic solver. Another way is to solve numerically using the root function.
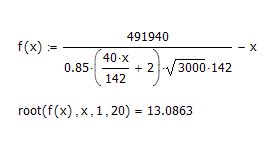
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Richard and please forgive my ignorance as it has been 30+ years since I sat in an algebra class, but I am going to take a shot at what I think is going on here . . .
Is the " - x" at the end of the function is to set the equation equal to zero? and the "root(f(x),x,1,20)" is requesting that MathCAD find the roots of x in the defined function "x" , totally guessing now, but is the "1,20" telling it to go through 20 iterations?
I feel the power, but I am just not one to push the "I believe" button without having a firm understanding of what is going on . . . . Thanks again for your input and help. Others feel free to correct me if I have strayed from the right path
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is the " - x" at the end of the function is to set the equation equal to zero?
Correct.
"root(f(x),x,1,20)" is requesting that MathCAD find the roots of x in the defined function "x" ,
If you mean the root of the function f(x), yes. I.e. it finds the value of x that makes f(x) equal to zero.
totally guessing now, but is the "1,20" telling it to go through 20 iterations?
It finds the root within the range x=1 to x=20. You could of course use other numbers, as long as they emcompass 13.08.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Alan, that got me to a correct answer, but . . . can it be done using the variables so that I don't have to manually plug and chug numbers?
I tried using this process with the variables and it solved for something, but it got ugly . . .
I removed the " *psi" from the f'c in the denominator to see if that would help, but to no avail . . .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolic solver does not understand units. If you are using units use the root function, which solves numerically.





