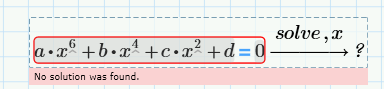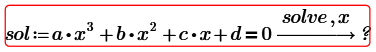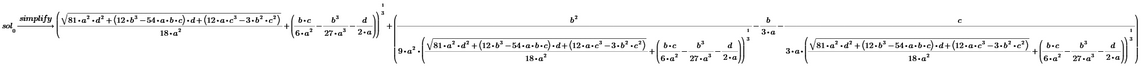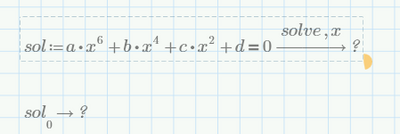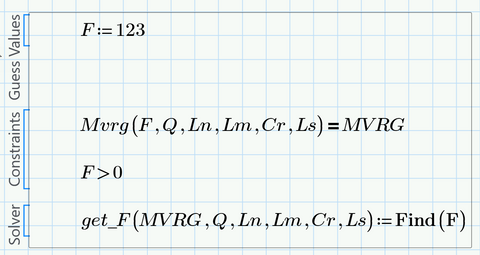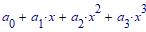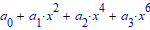solve equations symbolically

[Marius_P]

Hello,

I would like to get some help from you in regards to an equation that I would like to solve it symbolically.

Please find attached the file, which is on PTC Mathcad Prime 7.

Please let me know how to improve the equations in order to be able to find a relation for x.

Thank you,

[Cornel]

Your first expression is nonlinear type (because of that sqrt which has the x variable inside the sqrt):

and therefore  it's not so easy to find out the solutions. I don't think the solution will help you much even if Mathcad or other math software could find the solution for x. Maybe better, give values for the other variables, plot that expression according to x and read from the graphs what interests you.

Your second equation:

is of type:

But, at least Mathcad, cannot find solutions for such equations. Although I don't know if there are closed form solutions for equations of degree > 4. But if I'm wrong with this statement, others can correct me.

[Marius_P]

Hello Cornel,

Thank you very much for your feedback.

Actually, the 2nd equation is the exactly the 1st one after I eliminated the sqrt and I grupped the terms.

I ploted the transfer function for different values of lm, mvr, ls,cr, and q, and from there can be read x, but I thought that I can get a symbolic formula that I can use in my worst case calculations where the variables of the 6th degree equation varies between a min and max value.

Thank you 

[Cornel]

Look what the solution looks like for a polynomial of degree 3:

EDIT:
For a polynomial of degree 6 Mathcad probable will think at infinity:

[Cornel]

So, do you want one of the symbolic solutions of that 6th-order equation, and with that symbolic solution to further do some worst case analysis, correct?
Anyway, if you really want to get the  symbolic solutions of that 6th order equation, probably the most appropriate would be to use another math software (for example Wolfram Mathematica, Maple, Matlab) and see if you manage to get the solutions with these softwares. If you don't succeed with these software either, then you have to try something else...another way to achieve what you want to achieve.

[Werner_E]

As your simplified second equation shows, what you ended up with is a so called bi-cubic equation, which can be transformed to a simple cubic equation by substitution (y=x^2). A cubic equation is solvable symbolically (Cardano formula) and Prime should be able to do so. But as Cornel had shown, even using simple coefficients result in a rather huge expression for the solution (he only showed one of the three possible solutions).

Given the much more complex (not in the sense of non-real) coefficients in your equation, chances are that Prime will(should?) be able to solve that cubic equation but refuses to display the symbolic results as of their size. I haven't tried, but if thats the case you could turn the result in a function in all variables involved and use this function for further calculations.

But if you (as I guess) don't really need a symbolic solution but rather want to find the value of F for a given result value of the function Mvrg(), you could define a function using Primes numeric methods, either use a solve block or the root function.

Using a solve block:

The root function can be used in two different ways:

1) by providing a guess value (similar to whats needed when using a solve block)

2) by providing a range of F-values with a solution in between

You may consider adding n as an additional argument to your function Mvrg() and also to the function get_F()

[LucMeekes]

"Mathcad, cannot find solutions for such equations"...? Correction!

Mathcad (11) can, Prime cannot.

To give you an idea, the solution to

is

:

Likewise

can also be solved, with as result:

Success!
Luc

[Cornel]

In fact it seems that Mathcad Prime can find the solutions for that equation of 3th degree (of course, not so easy - Mathcad Prime needs to think a little bit), but Mathcad Prime cannot find the solutions for that equation of 6th degree...But as Werner said above, that equation of 6th degree, in this case - fortunately, can be reduced at an equation of 3th degree.

It would be interesting to know how one could deduce the solutions for polynomial equations of order 3, 4, 5, 6, when Mathcad can no longer deduce itself...

[LucMeekes · Accepted solution]

Have you ever considered to use the function polyroots() ?

You can go up to order 99.

Success!
Luc

[Marius_P]

Hello Luc,

Actually, I planned to try it.

Thank you,