Hello, Everyone.
From :
.PNG)
The question : What does _n mean ?
Thanks in advance for your time and help.
Best Regards.
1 ACCEPTED SOLUTION
Accepted Solutions
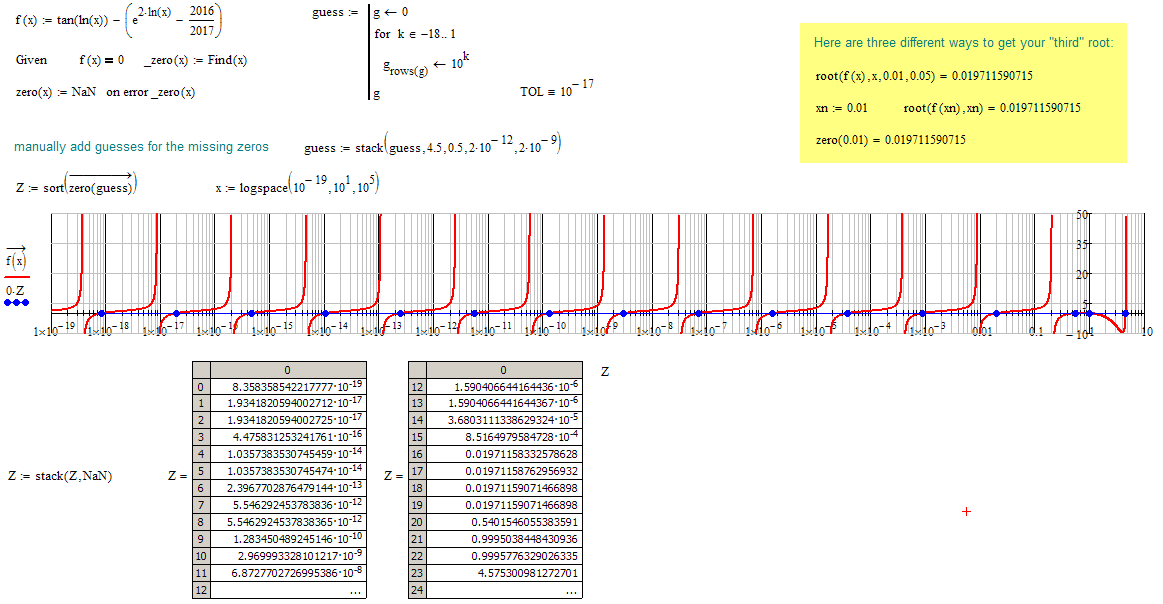
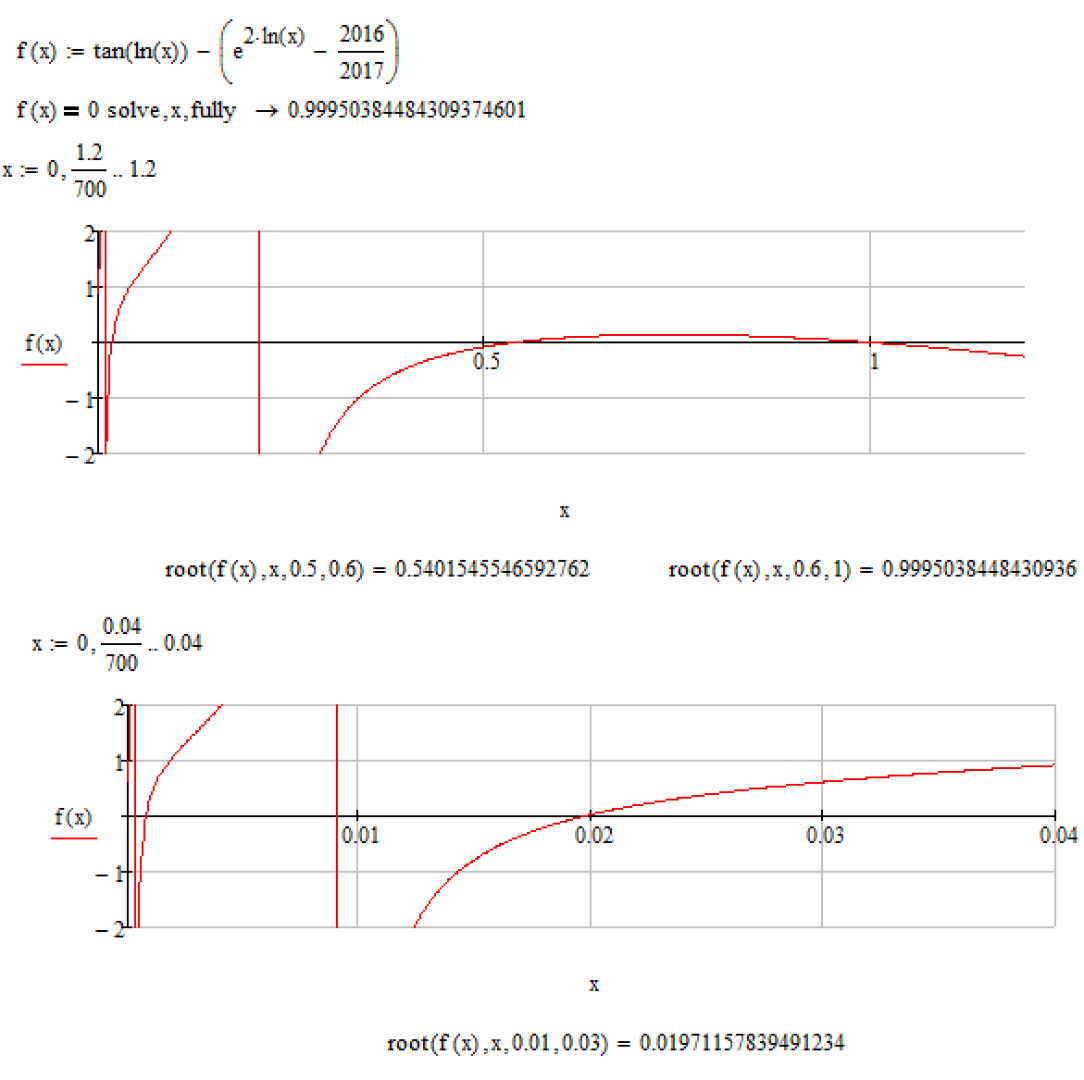
The question : how many real roots does the f(x) = 0, the above, have ?
Looks like its quite a huge number 😉
Find also three different ways to get your "third" root.
Welcome to numerical algorithms! Ever so often they don't converge or are very sensitive concerning the guess values.
You may also chose among a couple of different algorithms^if you use a solve block! Right click on the word "Find" and then chose one of the three offered nonlinear algorithms or mess around with the options offered. You will see that most of the time Levenberg-Marquardt (which is the default) is the best choice.
Also the setting of TOL can influence the solver and setting it to a level too low might make the solver fail.
You can also see (look at the values in my vector Z) that different guess values often result in slightly different values for what sure is the very same solution. Numerical inaccuracies is something you have to live with when you deal with numerical approximations.
Guess that Mathcads symbolics was trying to find more solutions but was not capable enough to find 'em.
It should not show you the _n as its meaningless in this case. You may call it a bug.
I remember we already had a lengthy discussion where I tried to explain to you that powers, roots, logarithms in the domain complex have an infinite number of results because you always can add integer multiples of 2 pi to the phase of a complex number and that Mathcad most often is no able to return all those solutions.
For example
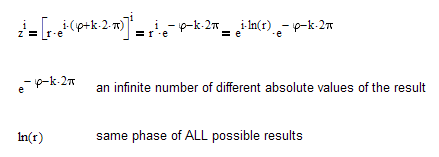
So possibly internally muPad applies that principle but is not able to succeed in your example.
Sometimes it succeeds but fails when it comes to simplifications or when demanded to show the results in rectangular mode:
In this example you could see, where the _n probably stems from and was accidentally left over.
Did you already notice, that Mathcad and especially also muPad are not perfect 😉
ADDENDUM:
In case you are in search for other solutions to your equation, you might use the numeric solver(s) (solve block, root function). Of course you have to live with its numerical limitations.
I greatly appreciate your time and help, Werner. 
. Especially, the ADDENDUM. ( I'm new with root( ) function. )
.PNG)
Is there a way to find the Max root directly, as the above ?
Best Regards.
I just played around and it wasn't that difficult as expected.
The expression simplifies (assuming real x) to
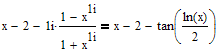
but I was not able to convince Mathcad/Mupad to do this for me.
When I start with
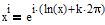
I end up with
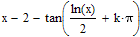
which of course is because of the periodicity of tan the very same as
and so there is no need to copy with various integers k (or _n).
The zeros of this function can only be found by numerical approximations and maybe thats the reason why the symbolics fail.
Anyway, even with this simpler function I found no way to convince Mupad to give me another solution than the 2,49..
Using Mathcads numerical methods you can get a lot of different solutions, but you can't be sure that you will get all (within a given range). Its just a matter of chosing the guess values.
I'm very v...e...r...y with your this answer. Thanks for telling me : rectangular operator ( I'm new with this )
.PNG)
And especially :
.PNG)
Thanks once again.
Best Regards.
Loi
Loi Le wrote:
I'm very v...e...r...y with your this answer. Thanks for telling me : rectangular operator ( I'm new with this )
.PNG)
Clever and tricky, to use one symbolic evaluation inside the other 😉
Keep in mind that we are using numeric methods later and they lack accuracy. Furthermore the results depend a lot from the guess values and you may have noticed, that one of the solutions is missing (0.115) while others occur more than once. You might want to play around and find a better suitable vector of guess values.
To visualize it would be best to use a logarithmic scale:
Happy New Year!!
Hello, Werner.
From :
.PNG)
The question : how many real roots does the f(x) = 0, the above, have ?
Happy New Year 2017.
Best Regards.
Loi
The question : how many real roots does the f(x) = 0, the above, have ?
Looks like its quite a huge number 😉
Find also three different ways to get your "third" root.
Welcome to numerical algorithms! Ever so often they don't converge or are very sensitive concerning the guess values.
You may also chose among a couple of different algorithms^if you use a solve block! Right click on the word "Find" and then chose one of the three offered nonlinear algorithms or mess around with the options offered. You will see that most of the time Levenberg-Marquardt (which is the default) is the best choice.
Also the setting of TOL can influence the solver and setting it to a level too low might make the solver fail.
You can also see (look at the values in my vector Z) that different guess values often result in slightly different values for what sure is the very same solution. Numerical inaccuracies is something you have to live with when you deal with numerical approximations.
.PNG)
Yes, Mathcads symbolics does a very nice job in returning ALL solutions or all solution in a given range, when the equation is solvable algebraically/analytically:
But Mathcads symbolics fails miserably when the equation is not solvable exact (and most equations we have to solve in real world problems aren't) and it has to resort internally to a numerical algorithm. Then we have no way to change a guess value or convince Mathcad to return a solution within a given constraint. Mathcad/MuPad selects ONE of the many possible solutions and presents only that, nothing else. Thats a big weak point and I am not sure if Maple in Mathcad 11 did a better job.
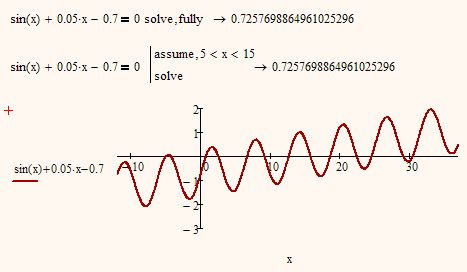
So in this case its better to do without the symbolics and use Mathcads native numerical methods (solve block, root) as shown in my answer above (Re: solve, fully and _n ?).
OK, anyway. Mathcad is fine, but now its just 4 hours until 2017, so lets open the first bottle! Good Luck to all of you!
