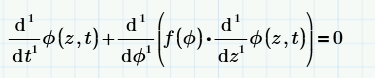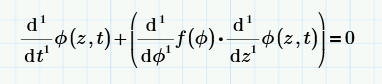Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
solve partial differential equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
solve partial differential equation
Hi,
I am trying to solve the Kynch sedimentation process. For that, I need some help solving PDE with certain initial and boundary conditions. The objective is to get volume fraction (ϕ) in terms of height (z) and time (t). I am not really sure on how to go about doing this. It would be helpful if someone could take a look at it.
Thanks.
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You appear to be using phi as a variable and as a function at the same time.
That is begging for trouble. You have to clear this up before you can begin to solve.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I have followed the equations given in the paper. Kindly check the attachments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To my opinion the paper uses inconsistent formulation.
At one time f is a function of just phi: "f(phi)".
At another point it is a function of two variables: "f(0,t)".
Mathcad, nor Prime will be able to work with that.
Success!
Luc
P.S
In your usage of Prime, with the derivative, you can leave the 'order' of the derivative blank if it's just 1 (It's only needed for second and higher order derivatives). That 'll help with readability.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Since df(ϕ)/dϕ=V, can I just put V*dϕ/dz instead for the second part of the equation. Will that help? Other than that, I am not really sure on how to proceed.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think that would help.
Now go and look up the information on 'PDEsolve' in het Prime help and apply it to your system.
Don't hesitate to come back here (with an attached Prime sheet) if you run into trouble.
{I don't have full Prime, 'cause I never wanted to pay for it; hence I'm limited to 'Express', which doesn't do PDEsolve. But I can view your files with no problem.}
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
PDESolve is part of real Mathcad (that is version 15 and below) for a long time, but as far as I know its not implemented in Prime.
In Prime concerning PDEs we are restricted to the use of the command line solvers.
"numol" for hyperbolic and parabolic PDEs and "multigrid"/"relax" for elliptic ones.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I thought I'd better try is symbolically...:
So we have an expression for the function phi.
Now from here you should be able to solve the two remaining constants a[0 & a[1 and subsequently find out if this function describes the behaviour you're looking for.
Success!
Luc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi LucMeekes,
Sorry for not being able to reply a little sooner. I am a little confused by how you got square of d/dz ϕ(z,t,V,a) in the pde. Shouldn't it just be d/dz ϕ(z,t,V,a) as per the original equation. Kindly clarify. I think I follow the rest.
Also, my guess is your soln is in mathcad 15 and not prime. Any ideas on how to transfer it into prime 4.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@arnair81 wrote:
Hi LucMeekes,
I am a little confused by how you got square of d/dz ϕ(z,t,V,a) in the pde. Shouldn't it just be d/dz ϕ(z,t,V,a) as per the original equation. Kindly clarify.
That's simple.
The original equation given (by you) was NOT (something like):
But:
Which means that when the
d/dphi of f(phi)
changed to
V * d/dz of phi(z,t)
the square of d/dz of phi(z,t) emerged.
If I look at the article that you took the formulae from, the situation doesn't get much clearer.
Considering that for the derivative of f(phi) the notation f'(phi) was used, one could even argue that it should have read:
d/dt of f(phi)
instead of:
d/dphi of f(phi).
I think you are more an expert on the subject at hand, so you should guide as to what the PDE should be. After that, I can help you solve it.
To get the (eventually resulting) formulae into Prime, you'll just have to retype them, or use the Mathcad to Prime converter. Note that you might need to do some rework after conversion.
Also note that, because (I think) you are a licensed user of Prime, you are entitled (=licensed !) to install and use Mathcad 15 on your PC. After installing Mathcad 15, for licensing point it to the very same license file already on your computer that you used for licensing Prime. You'll need Mathcad 15 installed if you want to convert any Mathcad (15 and before) files to Prime. (There's no backwards conversion. That is, there's NO tool whatsoever to convert a Prime sheet to a format supported by any previous Prime version, or Mathcad version.)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi LucMeekes,
Sorry, I am still a bit confused. The original equation is given by dϕ/dt +df(ϕ)/dz=0. In the equivalent form, we can write dϕ/dt +(df(ϕ)/dϕ)*dϕ/dz=0. Now f(ϕ)=ϕ*V. So shouldn't the final PDE be dϕ/dt +V*dϕ/dz=0 since df(ϕ)/dϕ=V.
I am relatively new to Mathcad. So far I have only used prime (version 2.0 and up). I do have Mathcad 15 and I find it to be bit different (slightly confusing) to prime. That is why I asked for a way to convert it to prime. Thanks for the help.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, I made a mistake: read one thing, interpreted as another.
You're right. The PDE, simplified by knowing that f(phi)=phi*V, should read:
d/dt of phi(z,t) + V * d/dz of phi(z,t).
I'll see if I can make this thing work.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
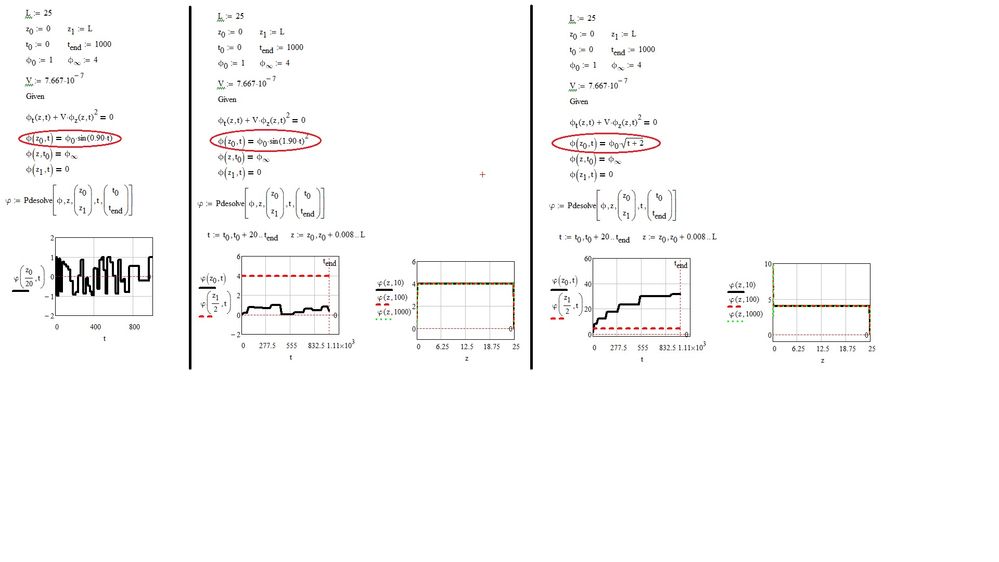
I believe the boundary condition should be
ϕ(z,t0,V,a) = ϕ0 (initial condition) - uniform volume fraction throughout the mixture initially
ϕ(z0,t,V,a) = ϕinfinity for t >0 (BC1) - sedimentation starts and volume fraction at the base starts to increase to final value.
ϕ(L,t,V,a) = 0 for t>0 (BC2) - concentration at surface z=L is 0 as sedimentation starts (clarification).
I think you have it slightly mixed up.
The settling plot should like what you see in the attachment. Any ideas?
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm. I can only hope this helps:
But none of these phi solve your PDE anymore !
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
So if none of the phi values solve the PDE, then it means that it is probably not the solution. That's a bummer. That kind of leaves me a bit stuck.
Can you please share your mathcad file with me.
Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Below are my attempts to find a particular solution, using MAthcad 15, to the equation, after having defined the boundary condition for ϕ: