Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
some questions of optimization with minimize
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
some questions of optimization with minimize
hi,everyone,i am a chinese,and my english is not good,this is my first time to communicate with others in english,i hope you can understand what I mean.
i have discused these questions on other branch,but still can't solve them,so i put it here for more help,the link address of the previous discussion
http://communities.ptc.com/thread/37201?tstart=0
Now,i have a lot of problems in my work.i want to fit the experimental data using the mathcad built-in function Minimize(also,i tried Minerr).the function is known,there are 56 parameters in this function,i want to find them by making the objective function to be minimized.but when i run it,it takes a long time;also,when i change the guess value from 100 to 0,the result change as well.
So,my problems are:
1,how to reduce the time(do not change TOL or CTOL)?
2,the result must be Local optimum,and how can i find global optimum?
3,the mathcad built-in function(minimize or minerr),can i see how it works,or the inside result?(i know the trace function,but it traces the independent variables(x,y) if i want to trace f(x,y),how to do that? i konw a stupid way,copy the independent variables(x,y),and then calculate f(x,y),but in my worksheet,the
independent variable is a matrix{9,9},it's too complex.are there any other functions that can trace f(x,y)?
thanks for your help
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
They may finish faster, but the sum of the squared residuals is bigger, so they didn't converge properly
You can speed things up somewhat by getting rid of some unnecessary vector multiplies. The biggest thing to fix though is that you can't have more parameters than data points. If you do, then you have an infinite number of solutions. Fixing that makes it a lot faster.
Your problem is really badly conditioned though. Changing the guess values by a very large amount does not change the fit very much. Your optimization surface also appears to have very many local minima, so changing the guess values results in different fitted parameters. The best way to address that problem would be to start with better guesses. This must represent a physical system, so surely you have some idea of what the approximate values of the parameters should be? Better starting guesses will also speed up convergence, because fewer iterations would be needed.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
1,how to reduce the time(do not change TOL or CTOL)?
Use minerr, not minimize. Currently, you are calculating the sum of the squares of the residuals as the objective function. You need to change that so that it just calculates a matrix of residuals (don't square and sum them). I started to do that in your worksheet, but realized it was going to be a lot of work, so I'll leave it to you ![]() . So you will have a function f(a) that returns the matrix of residuals, not the sum of their squares. As much as possible, you should do this using vectorization, not iterative loops. Define this outside the solve block. Also move your guess value calculations outside the solve block. Having them in the solve block is allowed in later versions of Mathcad, but they really should be above it.
. So you will have a function f(a) that returns the matrix of residuals, not the sum of their squares. As much as possible, you should do this using vectorization, not iterative loops. Define this outside the solve block. Also move your guess value calculations outside the solve block. Having them in the solve block is allowed in later versions of Mathcad, but they really should be above it.
In your solve block, put f(a)=0, along with your constraints, and terminate the solve block with minerr. Right click on minerr, and set it to Levebberg-Marquardt (the other options will not work with a matrix of residuals). Something to be aware of with minerr is that the constraints are treated as just another thing to be minimized. In other words, they are soft constraints, not hard constraints. To make them act as hard constraints weight them very heavily. So for example make your first constraint (a[1,1))*10^16=0.
Doing the above should speed it up a lot. The time required for a least squares fit goes up as the square of the number of data points and the square of the number of parameters though, so it's still going to take some time.
2,the result must be Local optimum,and how can i find global optimum?
There is no general solution to that. It's a non-linear problem, and all solvers are therefore iterative. The global optimum could be anywhere in an infinite sized parameter space, so no iterative approach can guarantee finding it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard,thanks for your help
i have tried Minerr before,it takes more time than minimize,of course,i choose the Levebberg-Marquardt.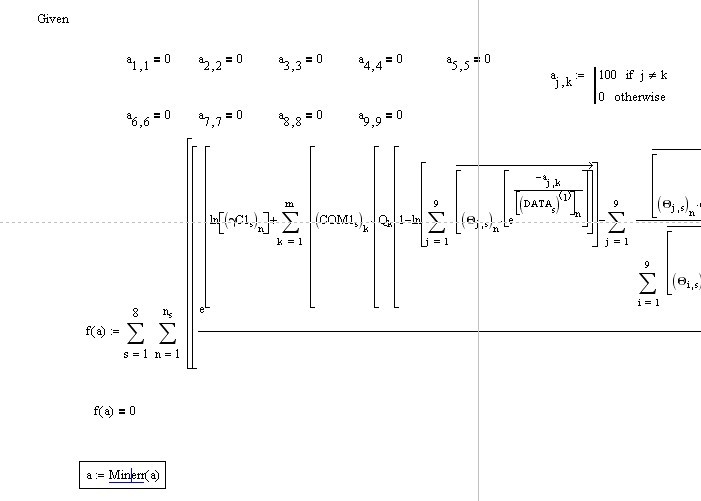
is there any mistake?![]()
i think the reason that it takes so long time is that the function may not fit the data very well,it can't reach the accuracy(TOL=0.001,CTOL=0.001),so it try again and again.if i can trace the value of f(a),maybe i can find the answer,but the trace function can only trace a.i am going crazy![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
is there any mistake?
Yes. Your objective function returns the sum of the squares of the residuals. Not only does this make minerr very slow, it sometimes does not even converge to the optimum solution. Your objective function should return a vector or matrix of residuals, not the sums of their squares. I think a nested matrix will also work, but I am not certain of that. Trust me. It will make a very big difference. This fact is mentioned in the help and the Quicksheet, but unfortunately it does not emphasize it enough.
i think the reason that it takes so long time is that the function may not fit the data very well,it can't reach the accuracy(TOL=0.001,CTOL=0.001),so it try again and again.if i can trace the value of f(a),maybe i can find the answer,but the trace function can only trace a.i am going crazy
It will minimize the sums of the squares (since it's a least squares routine!) but there is no guarantee that it will reach any given value. I do not think you can judge the quality of the fit just by looking at the sums of the squares of the residuals (the Chi Square) anyway. It depends on the magnitude of the data, and in your case the magnitude is quite large. I always plot and look at the fractional residuals. In your case, a series of surfaces, residuals/data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I take that back. They are not surfaces. I can't figure out what all the columns are though ![]()
The reason I tried to figure that out is that before performing the fit it's a good idea to plot the data and the fit with the guessed parameters. That way you can make sure that the guesses are at least reasonable. The closer the guesses are to the correct values, the faster it will converge.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your objective function should return a vector or matrix of residuals, not the sums of their squares. I think a nested matrix will also work, but I am not certain of that. Trust me. It will make a very big difference. This fact is mentioned in the help and the Quicksheet, but unfortunately it does not emphasize it enough.
dear Richard,do you mean this?

objective function should be f(a)=y(experimental)-y(calculated by the function that contains parameters a)?
i will have a try later.
thanks for your help and patience.![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
do you mean this?
Yes, that's the way to do it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
i tried,but it didn't work.![]() when i choose the L-M,it takes more time than the other two algorithms.
when i choose the L-M,it takes more time than the other two algorithms.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
i tried,but it didn't work. when i choose the L-M,it takes more time than the other two algorithms.
But I doubt very much it found the minimum with the other two algorithms.
Please post the worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
They may finish faster, but the sum of the squared residuals is bigger, so they didn't converge properly
You can speed things up somewhat by getting rid of some unnecessary vector multiplies. The biggest thing to fix though is that you can't have more parameters than data points. If you do, then you have an infinite number of solutions. Fixing that makes it a lot faster.
Your problem is really badly conditioned though. Changing the guess values by a very large amount does not change the fit very much. Your optimization surface also appears to have very many local minima, so changing the guess values results in different fitted parameters. The best way to address that problem would be to start with better guesses. This must represent a physical system, so surely you have some idea of what the approximate values of the parameters should be? Better starting guesses will also speed up convergence, because fewer iterations would be needed.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thanks.you are right,and really do me a big favor.
you are a great teacher. i have learnt a lot from you.![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's a way to speed it up by almost one order of magnitude.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes,that's a correct way..it leaves out a lot of calculations.thanks





