- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
two functions that depend on vector variables are giving error results
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
two functions that depend on vector variables are giving error results
To all,
the functions f1s and g1s are giving erroneus results, but i cannot find my mistake.
Please, if you can also check the evaluation of the integral below that will help as well.
thank you in advance,
Rogelio
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the functions f1s and g1s are giving erroneus results,
With "erroneus results" you probably mean that you did not expect nested matrices as result?
It looks like the vectorization in f1 of your function Delta is the reason for that behaviour, but at the moment its unclear to me what exactly is going on here as at first look I loose track as of your multiple nesting of different functions. At least I was not able to reproduce the effect with more simple examples.
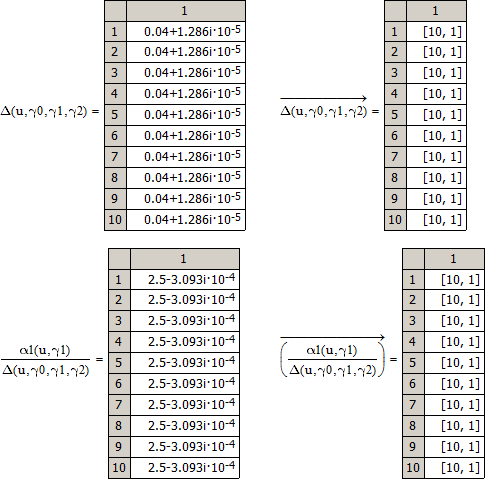
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, and here is a simpler example.
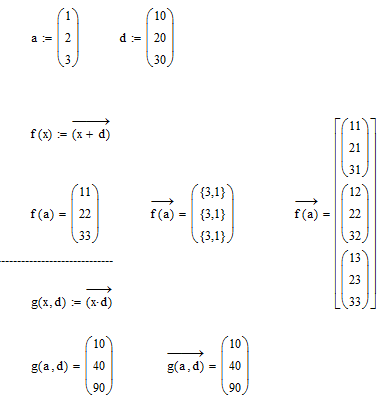
The vector d is hard coded at definition time in f(). The definition of f() is "take every element of d and add it to x" which would return a 3x1 vector. when f(a) simply adds the two vecors but if f() is called vectorized, Mathcad inserts every element of a singly in function f() and get back a 3x1 vector three times - so the result is a nested array.
In your file its the vector d consisting of ten eights which causes that mannerism in the definition of Delta.
One possible workaround is to make d a paremeter of your functions a sketched in the pic above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner,
i soon as i eliminated the vectorization in the f1s and g1s functions in the definition of the functions the problems seems to be solved.
i tried to run the pi function below the f1s and g1s function and now it says "pattern match exception".
Do you know what that means?
thank you in advance,
Rogelio
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your function returns a complex value, which is not compatible with the infinite limit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
it has worked for me in other cases of integrals with infinite limits, but i cannot find why it is not working now.
please, see attached file.
Is there any other way to do this kind of calculations?
thank you in advance,
rogelio
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As you increase the limit the imaginary part converges very fast, so that's easy. The real part oscillates, but it's clear what it will converge to eventually. It seems you also have a non-convergence problem if the limit is too high (those exponential terms, I think). I don't know what level of accuracy you require.





