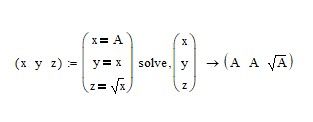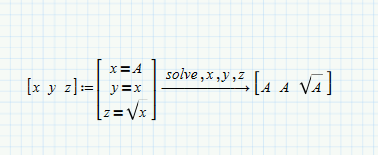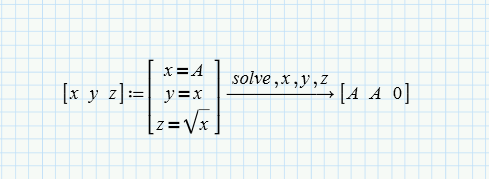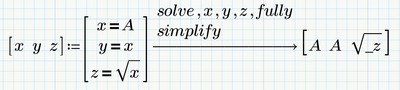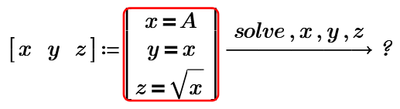Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
wrong calculation results with equations including root
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
wrong calculation results with equations including root
I encounter the wrong output of the calculation.
Equation
[x y z] := [x=A, y=x, z=sqrt(x)]T --> solve,x,y,z,
Of course sqrt is input as mathematical root actually.
The output becomes;
[A A 0]
The z value is wrong.
How can I fix this?
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What version of Mathcad are you using? And please upload your Mathcad worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Like this in Mathcad 15:
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My version is PTC Mathcad Prime 7.0.0.0, and the screen is like this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It sure should work the way you typed it in.
I suspect that Prime's unfortunate auto-label feature has struck again here.
Check the labels of ALL variables "z" if they are the same (all "variable" or all "-" meaning automatic) and change if necessary.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the reply. How should I input to confirm all variables?
If you post the screen shot of this command, it's highly appreciated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I've just gave it a try with Prime 6 myself, and for once, it's not the fault of the auto-label feature this time.
It appears to be a bug in Prime's new symbol processor. This was introduced with Prime 6, although the old symbolic still was available in this version. The old engine is no longer available in Prime 7, though.
If you feel like it and expect something from it, you may report the bug to PTC.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
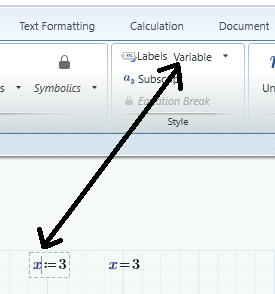
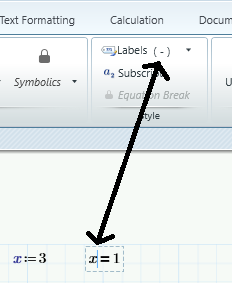
1. 'Select' the variable that you want to check, by placing the cursor into or next to it (see the thin blue vertical bar next to the first x).
2. Observe the label type (see other side of double arrow).
Every occurrence of x that you mean to be the same x, should have the same label type. If not: correct it by selecting the proper label type for it.
Better still: make sure that identifiers for different label types appear differently on the screen. Note that I have set the font colour for a variable to be dark blue. (I believe you cannot change the font of the automatic label type, so that 'll remain black, italic).
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
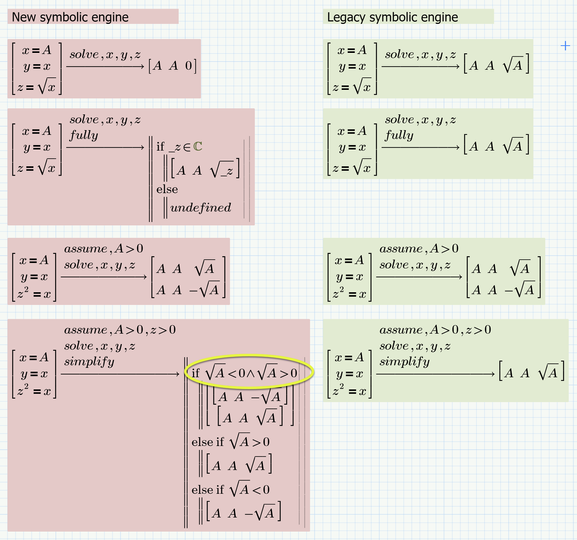
Unfortunately this time its another bug in the new symbolic engine.
If we use "fully" we see, that it thinks that z can be the square root of any arbitrary (complex) number _z.
And, yes, all occurrences of all variables are labelled the same!
The bug only occurs when using roots (no matter if we use the root symbol or exponentiation).
It works OK if we use something like z = x^3.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the instruction.
I checked this, and found out in the second matrix/vector that both x and y are variables while only z is (-).
I changed intentionally z as variables. BUT the result changes to 'no solution'.
Why? I can't understand...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Chances are you did not change the label of z in the "solve" command?!
That way the z in the last equation and the z you are solving for could be considered two different variables and so you actually try to solve for a variable which does not occur anywhere in the equations provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the advice. You are correct. I didn't change that 'z' to variables. Thus, I changed all 'z' as variables as well as 'x' and 'y'.
And the result becomes the same as the start....OMG.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@HA_10114654 wrote:
Thanks for the advice. You are correct. I didn't change that 'z' to variables. Thus, I changed all 'z' as variables as well as 'x' and 'y'.
And the result becomes the same as the start....OMG.
OMG, yes!
The new symbolic engine still is quite buggy and a work in progress, I guess.
Can't think of a suitable workaround neither. If you change the last equation to z^2=x you get two solution sets of course and I coukld not convince the new symbolics to chose the one desired using "assume" statements.
Here a comparison of the results given by the new and the legacy symbolic engine:
Given the region at the lower left I wonder if PTC could tell me the value of A with the square root of A being lower AND greater than zero at the same time 😈
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What happens if you change z to zz for all occurrences...?
I'm fearing that z is (mis-)treated as the set Z ...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
What happens if you change z to zz for all occurrences...?
I'm fearing that z is (mis-)treated as the set Z ...
Success!
Luc
I had a similar suspicion and had already tried it - but without a change.