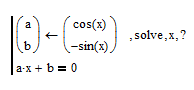- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
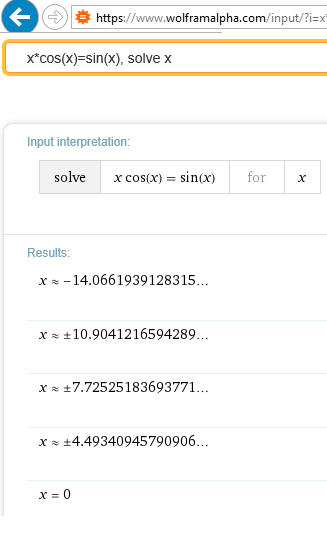
x.cos(x) - sin(x) = 0 solve , x ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
x.cos(x) - sin(x) = 0 solve , x ?
Hello, Everyone.
x.cos(x) - sin(x) = 0 solve , x ?
Thanks in advance.
Regards.
Solved! Go to Solution.
- Labels:
-
Math Homework
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
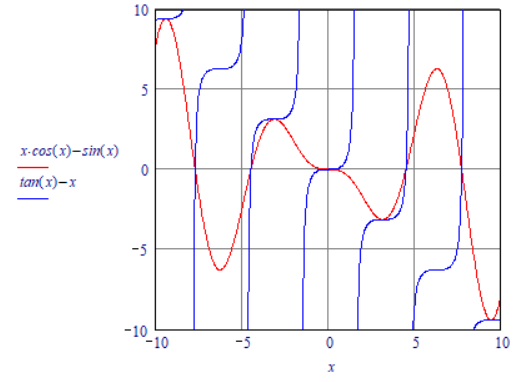
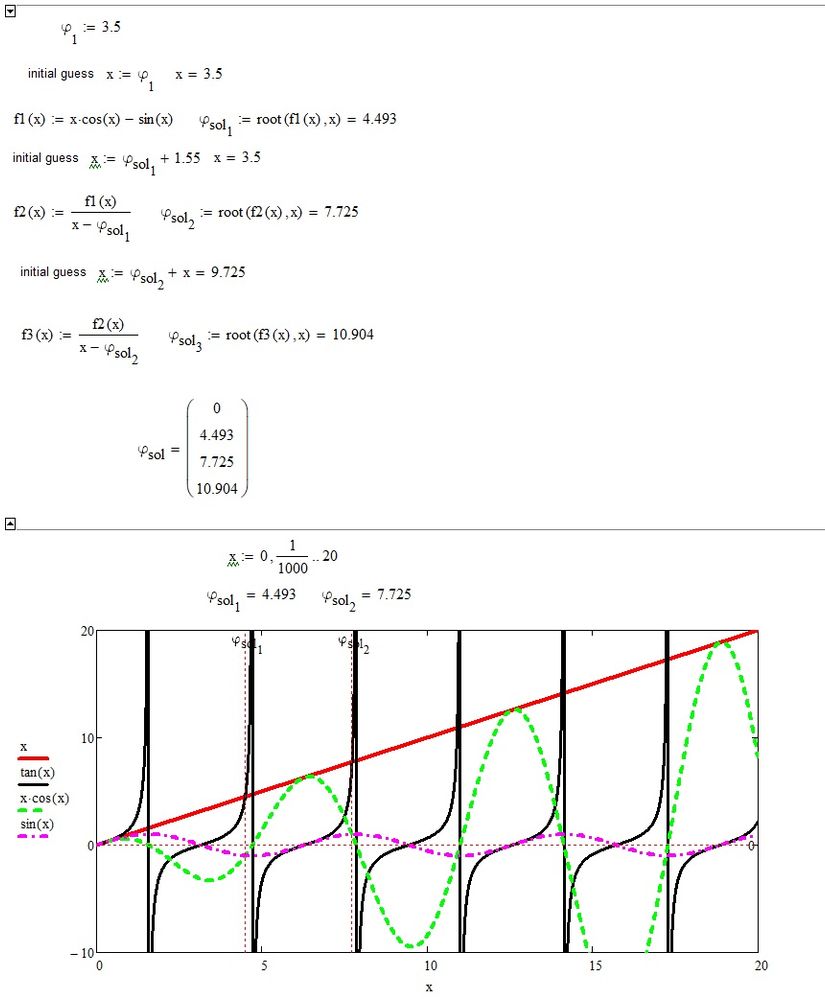
Is related to solving tan(x)-x=0:
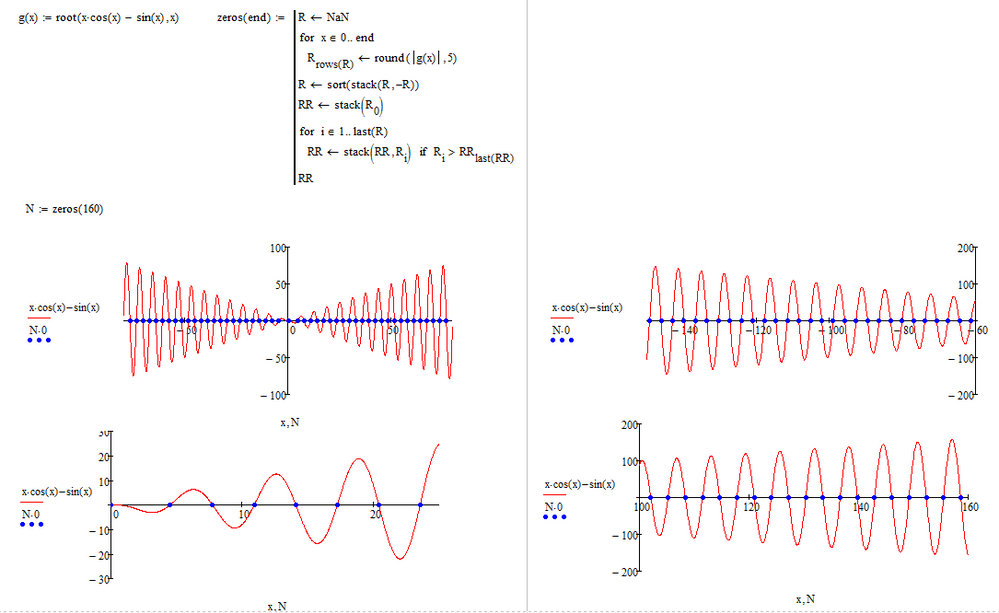
You should be able to find local zeros using the bracketed root function:
root(x*cos(x)-sin(x),-1,1)=
root(x*cos(x)-sin(x),-5,-4)=
etc.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolic "solve" will give you just the only exact solution (0).
All the others you'll have to find one by one using one of the numerical methods provided by Mathcad (solve block, root).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks Luc, F.M., and Werner. ![]()
![]() . Werner, I have a related issue, if you don't mind, please make correction the program function for a simple case :
. Werner, I have a related issue, if you don't mind, please make correction the program function for a simple case :
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You asked for something similar in another thread and I already explained that the program would have to be slightly modified to deal with the case when an interval hangs over the last limit you provide with your vector.
This should not have been that difficult.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner, Please make a correction for the program function, the above :
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Or writting a slightly different approach.
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just compare my program to the one you modified!
"R" instead of "r"
"last" instead of "rows"
Not sure what you think you get with your program, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Don't use functions posted here without fully understanding what exactly they do and why they were written the ways the were.
Would this help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're right. ![]()
And "could you attach *.xmcd ?"
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
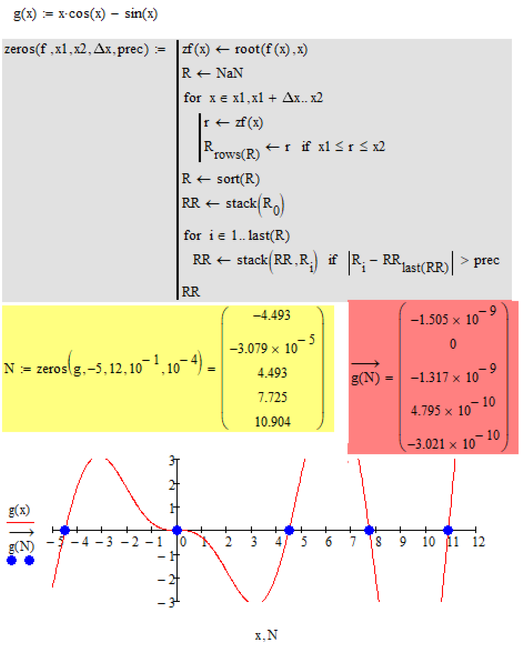
Werner, Yes this does help.![]()
![]()
![]() And I guess I'm still not fully understanding what exactly they do. And Is there any way to make the "red" becomes the "green" ?
And I guess I'm still not fully understanding what exactly they do. And Is there any way to make the "red" becomes the "green" ?
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
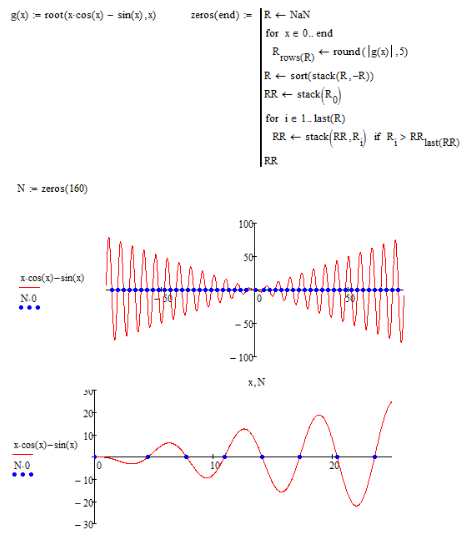
You may consider increasing the step width Delta_x or the last precision parameter.
The method used is brute force. All values from x1 to x2 with stepwidth Delta_x are fed as guess value in the root function and then the results are sorted. Values outside the range x1,x2 are eliminated and values closer as prec are considered the same.
root sometimes gives quite inaccurate values here like -0.01 while it should return 0. So you would have to change prec to 10^-2 or even higher which on the other side could mean that you are missing some other zeros.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
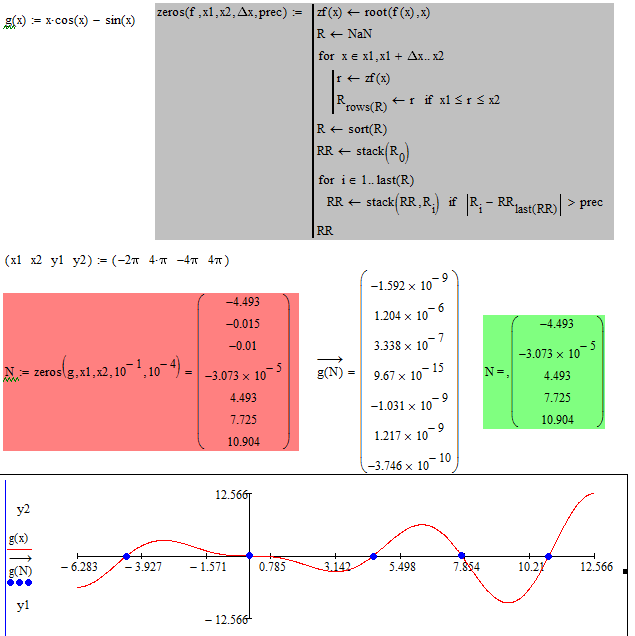
Here's a slightly different more stable looking approach using the interval variant of "root".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi liv107,
since it is a transcendent equation, you can solve it only numerically.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
More roots - not free