Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve non-trivial solution to a Matrix Function other than the solve block
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve non-trivial solution to a Matrix Function other than the solve block
Hi, everyone,
Right now I just want to find the non-trivial solution to the last equation above,
I can find that using the solve block, but since solve block cannot be used in programming,
I am afraid I have to find another way to solve a Matrix function with non trivial solution.
In Matlab, [eigenval, eigenvecs] = eig (K, M) would return to EV as eigenvecs, using the equation M*EV*lambda = K*EV, and it is easier for programming, say K & M varies.
So is there a way to solve non-trivial solution to a Matrix Function other than the solve block in Mathcad?
Thank you for your help!
Best
Shawn
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Matlab, [eigenval, eigenvecs] = eig (K, M) can return to both lambda and corresponding EVs, but not sure how to achieve it in Mathcad.
Would this help:


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have you tried "solve, fully" ?
But as long as you don't tell Mathcad that EV should be a vector or matrix, you will just get 0 as solution as this is the only solution of this equation - Mathcad treats EV as a scalar.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tried "solve, fully", but did not work as well.
So is there a way to solve Matrix equation, without using Solve Block?
I just want to make some preparation for the future programming work, if there is.
In this problem, lambda matrix is the eigenvalues of D=K-lambda*M,
then, using the Eigenvecs cannot come out with the right EV.
That's why I use this equation M*EV*lambda = K*EV to find EV.
In Matlab, [eigenval, eigenvecs] = eig (K, M) can return to both lambda and corresponding EVs, but not sure how to achieve it in Mathcad.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can't put a solve block in a program, but you can turn a solve block into a function:
phi(K,M):=Find(EV)
Then you can call phi(K,M) in a program with different K and M,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi, Richard,
Could you help me with some detail?
I tried to use the syntax in Solve Block, and defined a function, however, find function said "the function is misplaced. Move it to a solve block with one solve block function only.'
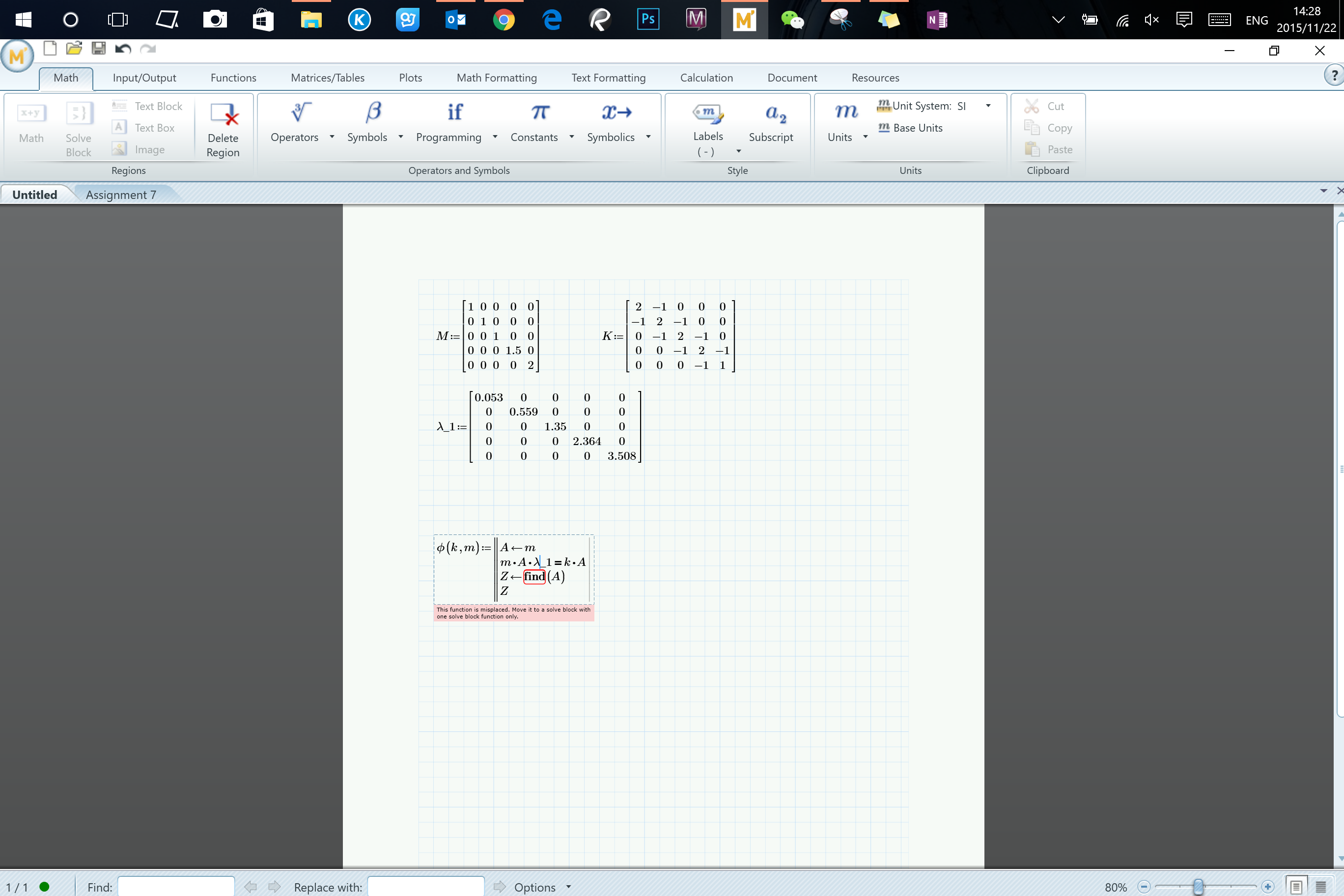
Anything to modify here?
Best
Shawn
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is what I meant:

There are two solve blocks, in cyan and yellow, that have been created as function definitions. The layout in Prime is a little different, but it works the same way. Once the functions have been defined they can be called anywhere later in the worksheet, including in programs. Note the use of symbolic evaluation of the first function to find all the eigenvalues, not just the one nearest to a guess value.
I don't suggest this is the optimal way to find eigenvalues and eigenvectors, but it shows what I meant.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi, Richard
But how to present the given and find block in Prime?
I tried both way, one is the syntax in 15 and the other is the solve block in prime.
Both shows the function Evals(K,M) cannot return to lambda
Best
Shawn
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Prime the correct form is the one on the right. Solve blocks can't just be typed into the worksheet (IMO a very annoying "feature" of Prime). But.....

I would call that a bug. It seems that in Prime the symbolic engine doesn't know what to so with a function that's defined in a solve block.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This works, as long as lambda is either not defined prior to the function definition, or you use clear.sym(lambda) immediately before the function definition if it is defined.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yeah! It works, and for the eigenvector, use the solve block will produce a valid solution this time.
Thank you so much, Richard,
I really learn a lot from your teaching!
Would mark both yours and Werner's as the correct answer.
May the force be with you two!
Best Regard
Shawn
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I really learn a lot from your teaching!
Glad I can help ![]()
FYI, In Prime that equation can be written in a simpler and more intuitive way. MC15 only has a column operator, so to getting a row requires a transpose, then the column operator, then another transpose. In Prime it just requires the row operator:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh, right, I just find that operator.
It is more convenient.
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Matlab, [eigenval, eigenvecs] = eig (K, M) can return to both lambda and corresponding EVs, but not sure how to achieve it in Mathcad.
Would this help:


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You are my hero!





