Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Help please with ODE solution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Help please with ODE solution
- Labels:
-
Calculus_Derivatives
-
Physics
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Did you forget to attach the Prime sheet with the error?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't agree with some of your equations. Attached is Prime 4 express. It has some problems too--Idon't like the angle plot, but my length plot is better than yours!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
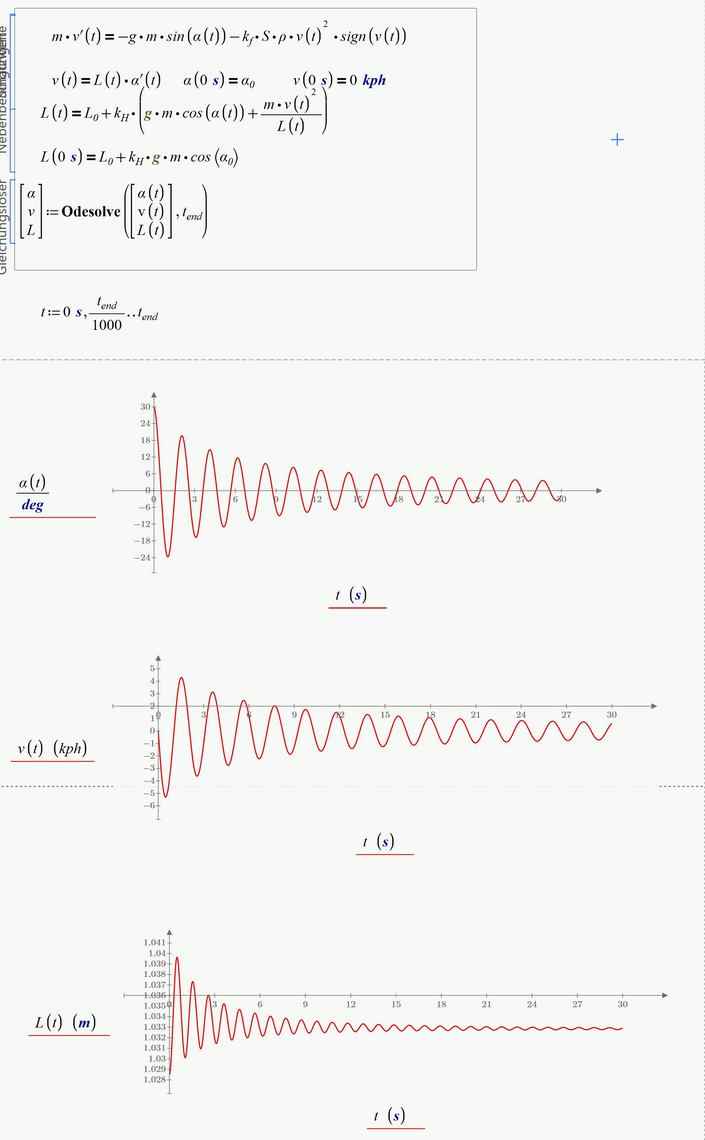
Here is what we get using Freds modified equation for L(t)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Note that I also questioned the sin(alpha) term in the first equation. Force due to gravity is vertical . . .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Obviously I was'n looking at your sheet with the necessary care.
But I guess Valery should know what exactly to change.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have no ode for L, no derivative. So you can't demand an initial condition for L The initial value L(0s) is dependent on alpha(0s) and alpha'(0s).
I have rewritten the block, nut still no success (at least we have a different error message now 😉
You may want to recheck your equations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Fred and Werner! See picture and attach!
One problem - Mathcad 15 sheet does not work. But after the converting into Prime - all OK! Why?
Solution without animation is not solution!
- Tags:
- anks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
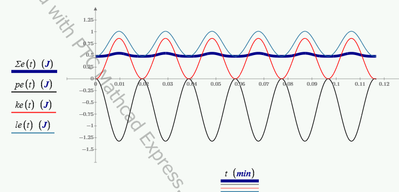
When alpha_0 < 7 deg - we have a balance of three energies
When alpha_0 > 7 deg - we have no balance of three energies
I know that alpha=sin(alpha) at alpha <7 deg!
See please The Prime 6 sheet in attach!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are three energies listed, but two of them are potential energy--the energy stored at the ends of the swing, and the energy stored in the compressed or stretched spring. These must be out of phase with the kinetic energy of the swinging pendulum; that's the nature of a harmonic oscillator (which this is.)
But that's not what your sheet shows
I can get to here
But something still isn't right.