Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Logistic Map and Ideal Random Number Generator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Logistic Map and Ideal Random Number Generator
by Mircea Andrecut
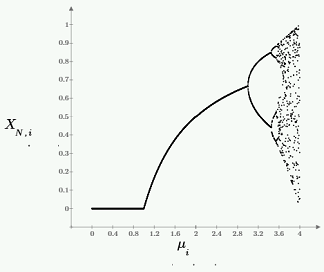
This worksheet using PTC Mathcad software describes the search for an ideal uniform random number generator, ultimately proving that the logistic random number generator simulates the behavior of the ideal uniform random number generator. Random number generators are important in simulating natural phenomena and in sampling data.
Numerical implementation of the ideal uniform number generator is discussed along with the linear congruential method which is frequently used to create random number generators. This worksheet also shares with you how to transform a logistic map into an aperiodic, not correlated and uniform random number generator. Using PTC Mathcad calculations, a uniform random number generator is created with an algorithm described in this worksheet. The algorithm is not correlated and is not aperiodic because of the numbers generated through the logistic maps.
This worksheet presents a simple method which transforms the logistic map in an aperiodic, non-correlated, and uniform random number generator. The logistic map generates an infinite chaotic sequence of numbers. A change of variable is used to make the distribution uniform. The numbers generated from this method can be passed through the Heaviside step function to simulate coin tossing.
Download and explore this worksheet yourself! You can download a free lifetime copy of PTC Mathcad Express and get 30 days of full functionality.
- Labels:
-
Statistics_Analysis


