Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
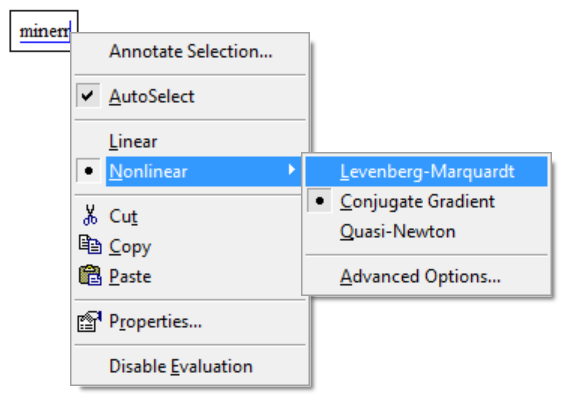
Minerr: Quasi-Newton, Levenberg-Marquardt, Conjugate Gradient?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Minerr: Quasi-Newton, Levenberg-Marquardt, Conjugate Gradient?
How to choose one of the Minerr Options? How initial values and Objective functions are affected by the selected Method? Are there Mathcad alternative solutions for non-linear regression of parameters?
- Labels:
-
Statistics_Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For non-linear regression (i.e. fitting a curve to data) you should use the L-M algorithm. The objective function should generate a vector of residuals (do NOT sum and square them!).
Mathcad really offers nothing else for this. The genfit function also uses the L-M algorithm, and is not as flexible as minerr. Simulated annealing was available at one point, with an extension pack, but that's unfortunately long gone. Is there a reason you want something other than the L-M algorithm? It's old, but it's very good.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am using Minerr for the non-linear regression of the parameters of a Volumetric Equation of State. I read that Quasi-Newton could be a good option for time consuming solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have a paper (although a very old one) that shows that the LM algorithm significantly out performs other downhill algorithms for fitting of data. The algorithm doesn't know what it's minimizing though, so the only difference between fitting data and any other minimization problem would be the number of residuals (when fitting data there are many: one for each data point). One reason LM is fast is that it adapts the step size as it iterates to the solution. It takes big steps to begin, and avoids overshoot by reducing them as it approaches the minimum.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, that's another desirable property of the LM algorithm. It inherently re-scales the parameter space to avoid the numerical problems Brent mentions. It seems the Knitro solvers probably don't, and that's why minerr works when minimize doesn't. I added a comment to that effect in the thread.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Richard,
In case of multiple object functions in a solve block, how the Minerr convergence tolerances work ( TOLL and CTOL )? Are the same criteria applied with LM or Quasi-Newton?