Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
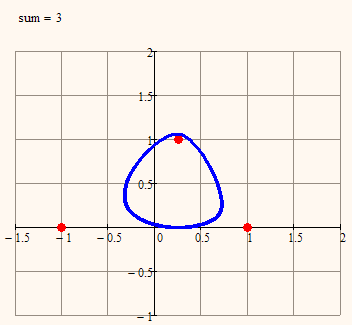
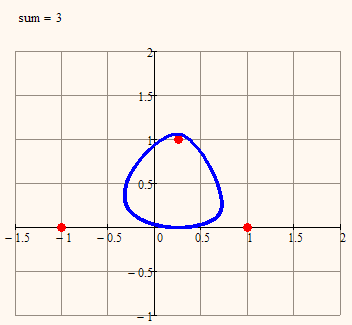
Seven math curves
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why not stay with the four basic operations and replace one of the points by a straight line?!
We have (with a=distance from the focal point and b=distance from the straight line):
a+b=const -> parabola
a-b=const -> parabola
a/b=const -> conic (a/b>1: hyperbola, a/b=1: parabola, a/b <1 ellipse)
a*b=const. -> ???
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Seven is one fine number - for not.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why be content with seven when you can have eleven or more ?
As it looks you like playing around with that kind of curves and also have the time doing so, her some additional ideas.
Stay with simple sum and used weighted distances. Something like two "focal" points 2a+3b=const when a and b are the distances from the "focals".
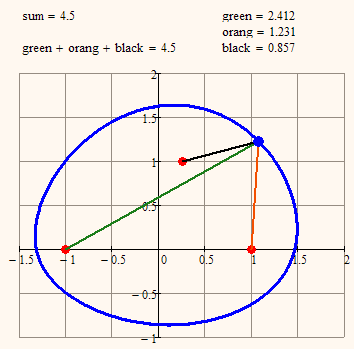
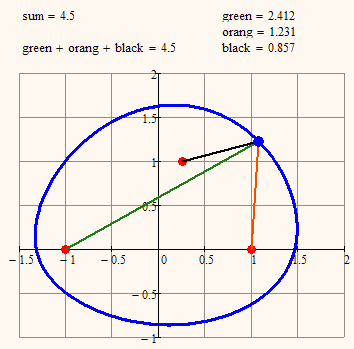
Or use more than one focal point. What about a curve, where the sum of the distances from three points is constant.
Regards
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As a starter here an animation demonstrating my last suggestion
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Werner.
One more thanks, that you not insert animation into your replies - now I am not in Moscow - I am on my dacha - not far from the place where Tchebyshev was born. Here Internet is very expensive.
See please Pafnuty Chebyshev - Wikipedia, the free encyclopedia
PS
Do you know how many built-in Mathcad functions has names based of persons.
Tcheb
rkfixed
J0
etc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Here Internet is very expensive.
I am sad to hear that. But embedding a streaming video won't help in this case as the data volume would be apprpox. the same - just better disguised as you get it bytet by byte. And I have learned from you that this PTC forum does not support the standard AVI container (or at least not if the video is using the standard codec utilized by Mathcad) and I would have to convert the video to a different format. It seems to me that attaching the original avi and providing a screenshot as I did ist the best solution in this situation.
And no, I don't know how many MC function are named after persons 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
> Here Internet is very expensive.
I am sad to hear that. But embedding a streaming video won't help in this case as the data volume would be apprpox. the same - just better disguised as you get it bytet by byte. And I have learned from you that this PTC forum does not support the standard AVI container (or at least not if the video is using the standard codec utilized by Mathcad) and I would have to convert the video to a different format. It seems to me that attaching the original avi and providing a screenshot as I did ist the best solution in this situation.
And no, I don't know how many MC function are named after persons 😉
Better to insert MOV video and attach AVI container! I try to do it here!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK Valery, I have a couple of questions:
- What is a dacha? Is that like a vacation?
- I see that Tchebyshev was made extraordinary professor in 1850 and then an ordinary professor in 1860. I would have thought that first you are ordinary, and then with practice you can possible become extraordinary. Please explain. Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Eric Seelye написал(а):
OK Valery, I have a couple of questions:
- What is a dacha? Is that like a vacation?
- I see that Tchebyshev was made extraordinary professor in 1850 and then an ordinary professor in 1860. I would have thought that first you are ordinary, and then with practice you can possible become extraordinary. Please explain. Thanks!
- What is a dacha?
A little country house.
- I see that Tchebyshev was made extraordinary professor in 1850 and then an ordinary professor in 1860. I would have thought that first you are ordinary, and then with practice you can possible become extraordinary. Please explain.
It is a big honor for me to compare me with Чебышев (more correct Чебыщёв)ю
But please explain your question. Ai no inglish very bэd.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, in common English usage extraordinary is superior to ordinary, So, it seems to us like he started out at a high level and then was demoted or downgraded to ordinary. I thought it was amusing, because I expect it must have meant something different to the university where he was teaching, and that our common understanding is not correct for Tchebyshev's position.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello everyone,
I ask permission to participate in the conversation and I would say that for me a dacha is a small cottage.
In the academic world, extraordinary professor is intended as a guest teacher or substitute, if I remember correctly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks F.M., that explains it. With that understanding it is easy to see how one could begin as extraordinary and then later acquire the full professorship and become ordinary.
Thanks also Valery and F.M. for explaining what a dacha is.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Eric Seelye написал(а):
Thanks also Valery and F.M. for explaining what a dacha is.
A dacha (давать - to give, дача, подача, подарок - a giving, a present) is a typical Russian word. Russian Tsar gave (давал, раздавал) his entourage land for the construction of the manor house.
Eric!
Welcome to the Thermal Engineering studies with Excel, Mathcad and Internet group
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Eric Seelye написал(а):
Thanks also Valery and F.M. for explaining what a dacha is.
A dacha (давать - to give, дача, подача, подарок - a giving, a present) is a typical Russian word. Russian Tsar gave (давал, раздавал) his entourage land for the construction of the manor house.
Eric!
Welcome to the Thermal Engineering studies with Excel, Mathcad and Internet group
Thank you Valery!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Valery,
A while ago you invited me to your community page for "Thermal Engineering Studies with Excel, Mathcad and Internet" but the link no longer works. Is there a new page? Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks from me too...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
As a starter here an animation demonstrating my last suggestion
Animation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
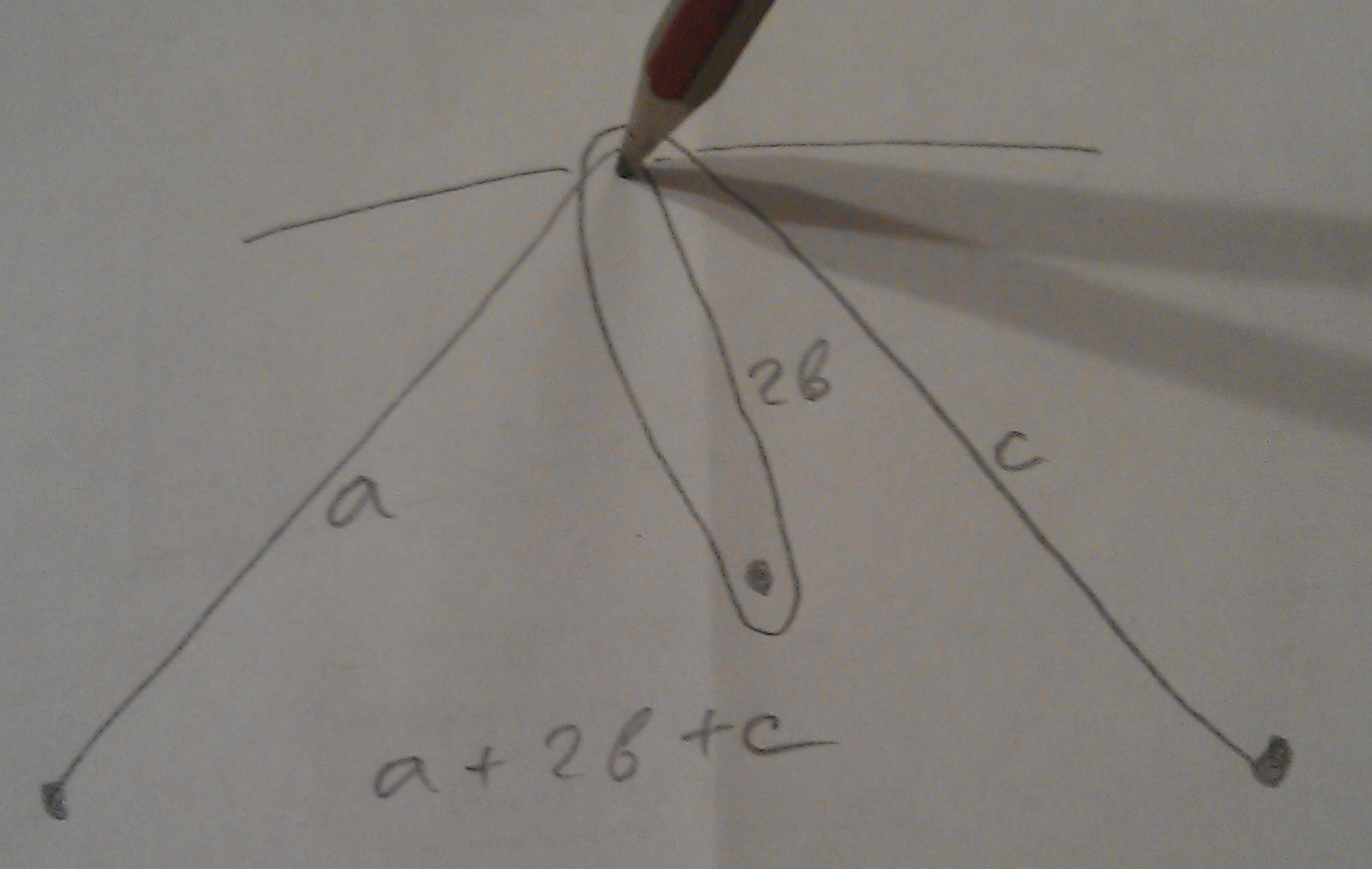
We can do it without computer:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
As a starter here an animation demonstrating my last suggestion
Hi Werner!
Create, please. this ellipse

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner!
Create, please. this ellipse
Here you are. Sigh!
.gif)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nile!
And what about you as coauthor of the article?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here ist the other one.
Have fun!
.gif)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From my new article
Ellipse can have more then 2 focuses - three, for example. These closed curves called n-ellipses or a person's name, their suggested curves Tschirnhaus(https://en.wikipedia.org/wiki/N-ellipse). This philosopher, mathematician and experimenter and is considered to be the inventors of European white porcelain, which have been producing in the town of Meissen near Dresden. You can offer this portselan factory, which operates to this day, in honor of the release Ehrenfried Walther von Tschirnhaus (1651-1708) made a souvenir plate of white porcelain with the shape and pattern shown abov3
У эллипсов может быть более двух фокусов – три, например. Такие замкнутые кривые называют n-эллипсами или по имени человека, их предложивших, кривыми Чернхауза (https://en.wikipedia.org/wiki/N-ellipse). Этот философ, математик и экспериментатор считается и изобретателям европейского белого фарфора, который стали производить в городке Мейсен недалеко от Дрездена. Можно предложить этой порцелановой фабрике, которая работает и поныне, выпустить в честь Эренфрида Вальтера фон Чирнхауса (1651-1708) сувенирную тарелку из белого фарфора с формой и рисунком, показанным выше.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> From my new article
In case you don't just want to play around with animations but are willing to invest time in some serious work on those curves, here are some links you might be interested in:
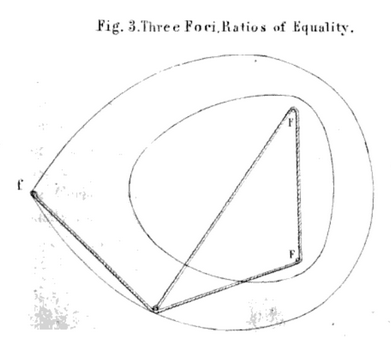
Here is a paper way back from 1846 and 1847 and I guess you recognize the ideas given there 😉 There is also a chapter on "trifocal curves" and their mechanical construction using a string 😉
https://books.google.at/books?id=zfM8AAAAIAAJ&pg=PA35
Here an interesting footnote concerning the above paper
https://books.google.at/books?id=QNosAAAAYAAJ&pg=PA89
Here is one of the figures from the papaer, showing the mechanical construction of a 3-ellipse
Some other readings:
http://www.mathcurve.com/courbes2d/cayleyovale/cayleyovale.shtml
http://arxiv.org/abs/math/0702005
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a second animation, varying the constant
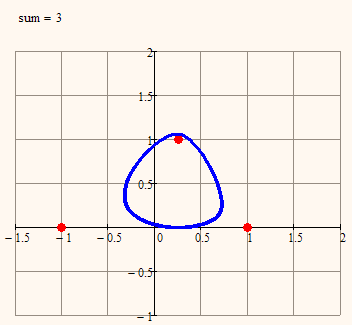
But beside all of this we shall not forget, that all these gizmos make only sense, if for these new(?) curves interesting properties (a closed parametric representation, arc length, encloses area), be them mathematical or other, are found.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And what about
a • b • c = const
or
a^b^c = const
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, so many variations possible. You may also ask for a+b-c or something like (a+b)*c or a/(b+c), or ....
But I am lacking the time (and interest) to deal with. Especially as it would be necessary to find some interesting properties of those curves, some possible applications in real life, or something like that to make better sense. Animations alone are nice but not enough. Really dealing with those curves would afford a lot more time to spend on.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
Here is a second animation, varying the constant
But beside all of this we shall not forget, that all these gizmos make only sense, if for these new(?) curves interesting properties (a closed parametric representation, arc length, encloses area), be them mathematical or other, are found.
WE
Better 2a+b+c, a+2b+c or a+b+2 c= constant!
Do you know why?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
Here is a second animation, varying the constant
But beside all of this we shall not forget, that all these gizmos make only sense, if for these new(?) curves interesting properties (a closed parametric representation, arc length, encloses area), be them mathematical or other, are found.
WE
Animation