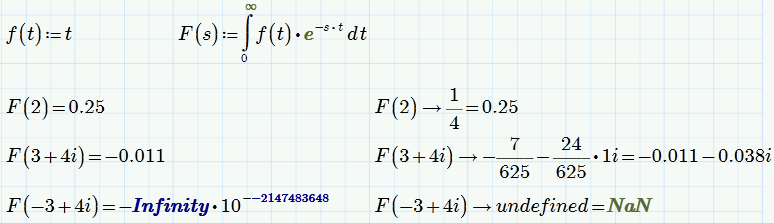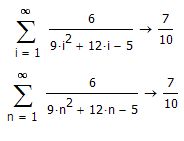Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolic Math in Mathcad 15 & Prime
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolic Math in Mathcad 15 & Prime
I see that Symbolic Math in Mathcad Prime is more correct than in Mathcad 15:
Do you know others examples?
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What I see in MC15:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
What I see in MC15:
Sorry,
now I see - it was an error of one my student - he used not correct symbol - fron this set:
Goto bugs - to this groupe http://communities.ptc.com/groups/mathcad-paradoxes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I see. So it's actually a proportional symbol, not alpha. ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Works correct (not more or lesss :-D) here in Mathcad 15, too.
Maybe your infinity sign is not interpreted as infinity because you type "infinity." for example?
Or you fooled yourself with one of your Str-Shift-K tricks (e.g. by typing infinity Str-Shift-K Space)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Actually, if you look closely that is an alpha, not an infinity. I noticed that before, but thought it was just a bad bitmap. Every other character looks fine though, including the infinity in the limit expression, so it's not just a bad bitmap.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad Prime 2.0
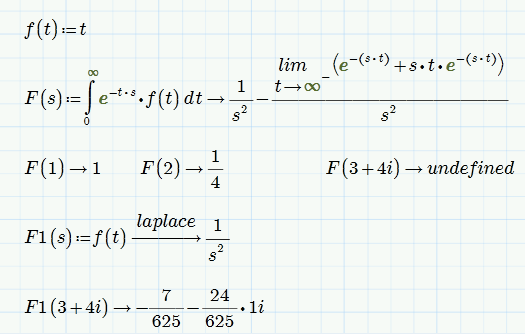
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Same effect here with Mathcad 15 (not surprising as they didn't change the symbolic engine).
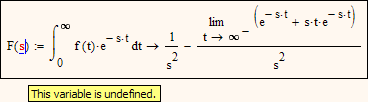
What I don't understand is the error message complaining that s is not defined as s is the formal argument of the function F. This results in the function F inot being defined and usable.
Concerning the result of your integral, Mathcad is correct adding that limit. The Laplace transform 1/s^2 is valid only for Re(s)>0 and Mathcad gives the appropriate answer using the modifier "assume,Re(s)>0":

But i agree that F(3+4i) should yield a result with your function F(s) and not "undefined".
I think its a bug in the symbolic engine which seems to have troubles evaluating some limits with complex values. The following limit should yield 0 for Re(s)>0 but doesn't:
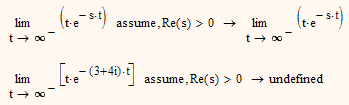
But it's interesting that Mathcad is able to evaluate the integral in picture2 correct using Re(s)>0 but fails with the limit.
It gets more mysterious if you define F(s) without following it by symbolic evaluation. Now the symbolic evaluation for specific values is correct but the numeric one has problems with complex arguments!!?? At least with Mathcad 15.
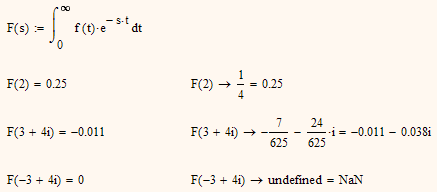
Slighty different in Prime2 but not really better: