Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
x^(1/ln(x)) - e = 0 . Find x .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
x^(1/ln(x)) - e = 0 . Find x .
Hello, Everyone.
Thanks in advance for your time and help.
Best Regards.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Very strange equation. All values of x are solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Viktor Korobov wrote:
Very strange equation. All values of x are solutions.
Sure! Why do you think thats strange?
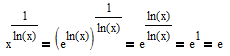
This is valid only if we implicitely assume that x is greater than zero and all should be done within the range of real numbers. Doing it in complex we get complex numbers, all with magnitude e and the arguments are k*2*pi/ln(x), where k is an arbitrary integer. This may be an infinite or a finite number of results, depending on if ln(x) is integer or not. As an example: if x=e^2 the expression yields either +e or -e. If x=e^4 we get +e, -e, +e*i and -e*i. For most values of x we will get an infinite number of results but whatever x may be, e is amongst the results in every case (for k=0).
Real or complex, x=0 is not valid in any case.
In the aforegoing thoughts I have not yet considered the ambiguity of ln(complex) at all.
Mathcad is not good in that kind of non-real-world "problems". It also has difficulties to solve the equation

You may think Mathcad can do better with a solve block when you add a constraint
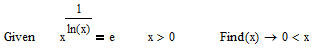
Is the result could be interpreted as "any positive x is solution", which would be correct. But thinking that the symbolic solve block use is curing all problems is an illusion as the following example shows:
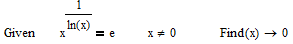
Mathcad is completely ignoring the constraint (as so often when we use the symbolics) and yields an invalid result.
Maple in MC11 was a bit better (no surprise):

but it was in no way perfect:
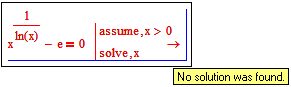
Thanks to the new modifier "fully" here even muPad does better:
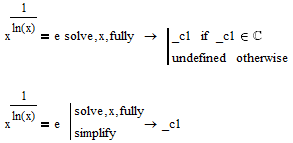
Its still missing to say "undefined if x=0"!
A funny one (while perfectly valid) is this one
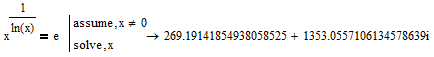
So as a conlusion my advice at LoiLe:
If you are trying to solve real world problems, feel free to use Mathcad and if you get stuck, come here and ask.
But if you are still learning and are just exploring the world of mathematics, as you once wrote, it could be better to do without Mathcad. Mathcad isn't a good escort on THAT way.
Mathcads results ever so often require you already having some sound knowledge of math and some "math common sense". Its not a teaching tool.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wolfram Alpha solves incorrectly?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Viktor Korobov wrote:
Wolfram Alpha solves incorrectly?
Obviously it does! Its not built for that kind of sophistry.
In the first case it should read "all values but 0". Its the same as (1/x)^(-1)=x is true only for x different from zero - the expression is NOT an identity. The same goes for x/x which is NOT equal to 1 (only if x does not equal 0).
And the "solution" in the second case, which actually IS an identity, should be that all values of x are solution. e=e sure is TRUE if x=17.345 🙂


